2.3.2.2 Divisores Resistivos

 

Este método de medición se usa para aportarle más rango de operación al voltímetro, como se demostró en la medición directa el error que posee no suele ser un inconveniente pero los equipos de medición tienen limitaciones, por ejemplo el fluke 179 es capaz de realizar mediciones hasta 1000 [V], pero otros equipos no son capaces de llegar a este valor o por otro lado contamos con sistemas mayores a 1000 [V] (un ejemplo pueden ser las redes aéreas de 34.5 [kV]).

Consta de usar un divisor de tensión resistivo el cual tiene como objetivo ampliar el rango de operación del voltímetro, usando una proporción de la tension total a medir, a continuación se podrá observar una comparación de los métodos de medición Directa vs medición Indirecta - Divisor resistivo. (Ya que al ser la medición directa un referente de todo estudiante es perfecto para mostrar las diferencias de este método de medición):

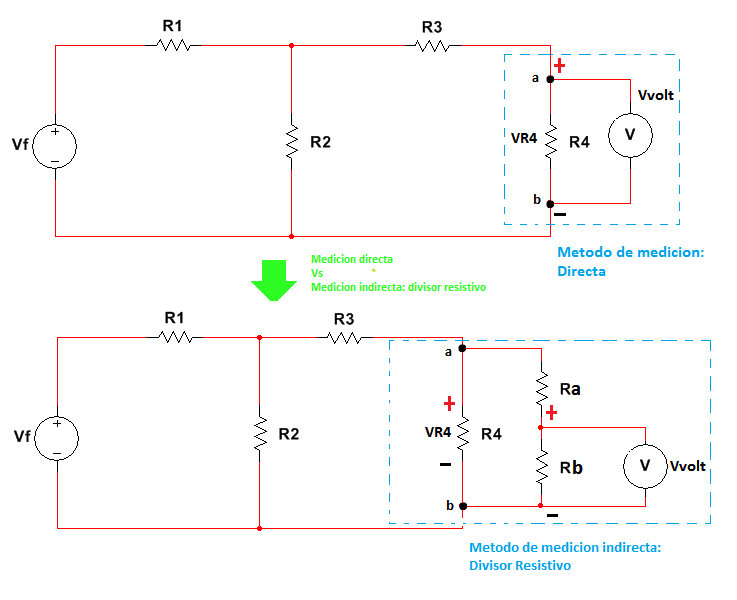
Figura 2.3.2.2.1 Medición Directa Vs Medición Divisor resistivo

Como es apreciable en la figura anterior, en el método de Divisor resistivo no solo interviene el voltímetro sino que además se encuentra presente un divisor resistivo compuesto por las resistencias Ra y Rb, todo el sistema se encuentra en paralelo respecto a los puntos a-b:

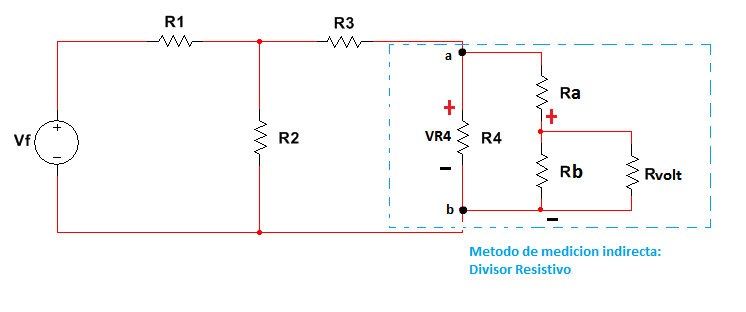
Figura 2.3.2.2.2 Medición Divisor resistivo con resistencia del voltímetro

Siendo Rvolt la resistencia que presenta el voltímetro dada por el fabricante la cual afecta el circuito en el cual se desea realizar un análisis.

Además el voltímetro no vera la tensión VR4 sino una tensión llamada Vvolt la cual puede ser conveniente para el equipo de medida, es decir VR4 puede ser tan grande que el equipo de medida es incapaz de medirla, pero por otro lado gracias a Ra y Rb el valor tomado por la tensión VR4 es tan pequeño como se desee.

Una ventaja importante de este método de medición es que se es capaz de realizar un análisis desde el error, el cual permitirá controlar el porcentaje con el cual el sistema de medición tendrá repercusión sobre el circuito

• Recomendaciones:

Estas recomendaciones se verán explicadas con profundidad en el concepto teórico.

• La corriente que atraviesa al voltímetro debe ser lo más pequeña posible.
• Para cumplir la recomendación anterior la resistencia Rb << Rvolt esto con el fin de que la corriente pase mayormente por la resistencia Rb.

• Concepto Teórico:

La medición de tensión como cualquier otra medición de una variable eléctrica partirá del circuito equivalente Thevenin de donde se quiera realizar la medición (esto con el fin de simplificar el análisis), en este caso se quiere realizar la medición de la tensión VR4:

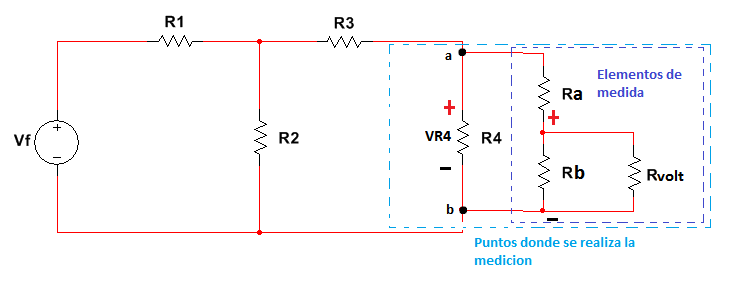
Figura 2.3.2.2.3 Elementos de medida

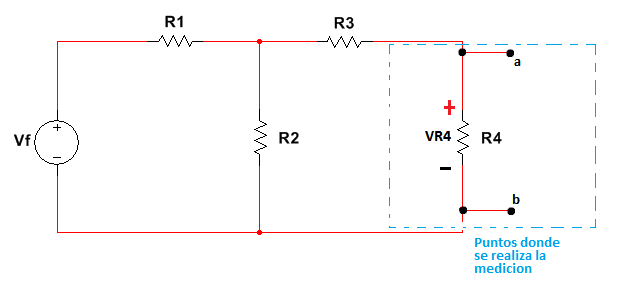
Figura 2.3.2.2.4 Ubicación puntos a-b

La ubicación de los puntos a-b estarán dados por el lugar donde se encuentran los elementos de medida (Voltímetro y resistencias Ra, Rb), y visto desde allí se hallara Vth y Rth respectivamente, es decir se extraen los elementos de medida y con el "nuevo" circuito serán hallados los valores.

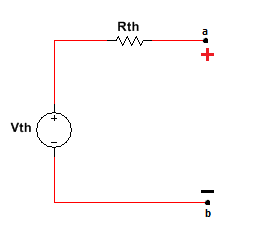
Figura 2.3.2.2.5 Equivalente Thevenin visto desde a-b

Es en este circuito donde se realizara el análisis incluyendo el sistema de medida y realizando los cálculos pertinentes para determinar los valores de:

• tensión
• Potencia
• Error relativo
• Error Absoluto
• Incertidumbre de la medida

De acuerdo a la teoría vista en circuitos D.C la tensión Thevenin y resistencia Thevenin son los valores vistos desde los puntos a-b, por lo que el voltaje Thevenin equivale a el valor convencionalmente verdadero de VR4.

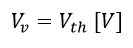
Ecuación 2.3.2.2.1 Voltaje VR4 verdadera

Este valor hará mención al valor verdadero o valor teórico.

Si se integra el sistema de medida en el circuito se obtiene el siguiente circuito:

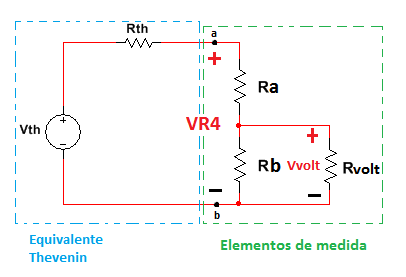
Figura 2.3.2.2.6 Equivalente Thevenin con sistema de medición

Realizando el análisis de tensión Va-b se obtendrá el valor VR4 medido del circuito.

Primero se determinara una resistencia en paralelo entre Rvolt y Ra:

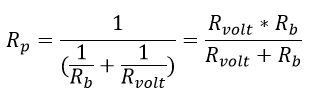
Ecuación 2.3.2.2.2 Resistencia paralelo

También se puede obtener una resistencia serie entre Rp y Ra:

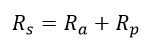
Ecuación 2.3.2.2.3 Resistencia serie

Por medio de un divisor resistivo se puede determinar el valor de la tensión VR4 medida:

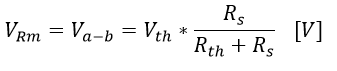
Ecuación 2.3.2.2.4 Resistencia VR4 medida

Para la selección de Ra y Rb además de ver como el sistema de medición afecta al circuito:

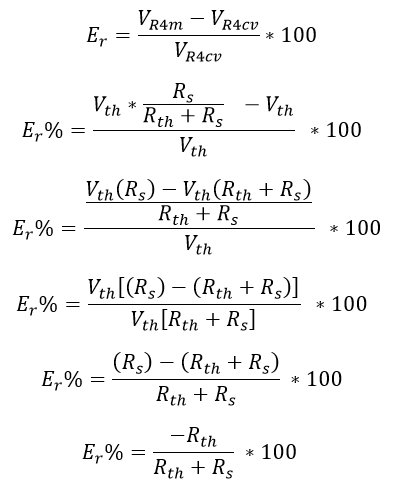
Ecuación 2.3.2.2.5 Análisis desde el error

Antes de pasar a la selección de la resistencia serie Rs es importante recalcar de este error la forma en la que afectan los elementos de medición (Ra, Rb y Rvolt resumidos en un equivalente Rs):

• Si Rth >> Rs el error tiende a acercarse a 1 por ciento ya que es la división entre dos números muy parecidos).
• Si Rth << Rs el error tiende a acercarse a 0 por ciento (ya que es la división entre un valor pequeño sobre un valor muy grande).
• Si Rth es igual a Rs el error será 0.5 por ciento (ya que es la división de un número (Rth) sobre su duplicado (Rs+Rth)).

Al ser Rs un equivalente serie se puede encontrar una limitación si se despeja para la resistencia paralelo:

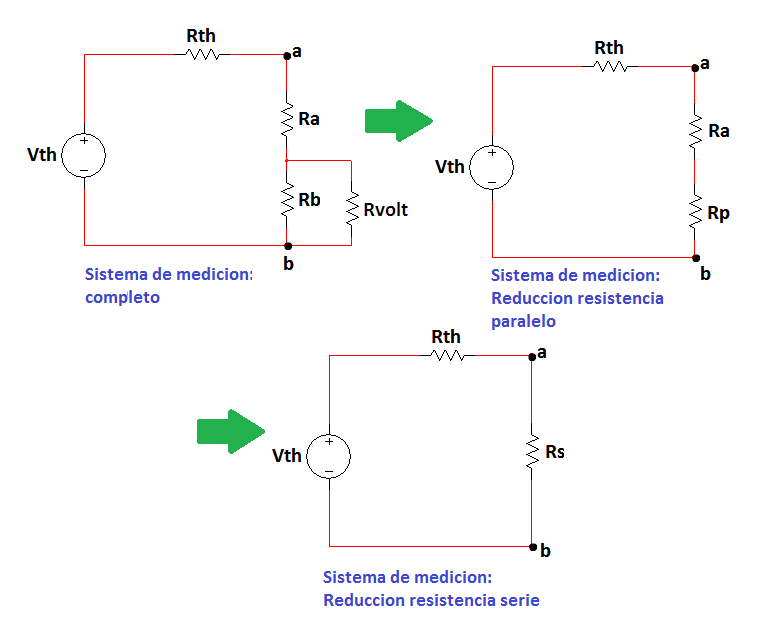
Figura 2.3.2.2.7 Sistemas de medición reducidos

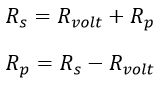
Ecuación 2.3.2.2.6 Resistencia paralelo

Aunque la resistencia paralela (la cual es una componente de la resistencia serie) este limitada gracias a su comportamiento (paralelo entre Rb y Rvolt) esto no significa que se posea un voltaje seguro y adecuado en el equipo, por lo que la selección de resistencias vistas desde el error puede ser algo peligroso.

Por otro lado se puede calibrar el sistema de tal forma que en el voltímetro se pueda seleccionar un valor de tensión, esto con el fin de realizar un análisis del error visto desde las tensiones y además brindar protección al operador del equipo.

Al ser la tensión Vvolt una porción de la tensión medida (Va-b o Vm para abreviar) se puede encontrar por medio de un divisor de tensión una forma de relacionar ambas, dando por hecho que se conoce el valor de Vvolt (valor seleccionado):

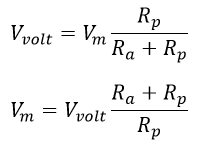
Ecuación 2.3.2.2.7 Relación Vm - Volt

Si se ve la parte resistiva como una relación de transformación entre Vm y Vvolt se encuentra la siguiente expresión:

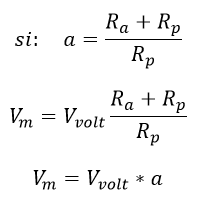
Ecuación 2.3.2.2.8 Relación Vm - Volt por relación de transformación

Ahora que se puede relacionar el valor de la tensión medida Vm con la tensión del voltímetro Vvolt ya conocida se puede realizar un análisis desde el error para así determinar una relación de transformación adecuada al error y la selección del error:

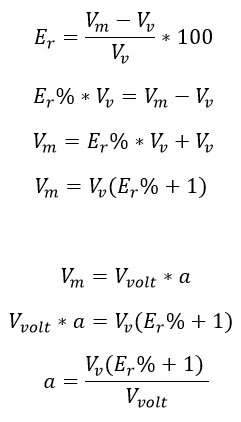
Ecuación 2.3.2.2.9 Relación de transformación

Esta relación de transformación estaría cumpliendo con una tensión en el equipo seleccionada (tensión Vvolt segura) y un error pequeño (menor al -1%) partiendo desde el error verdadero (Vv) por lo que se posee un control absoluto sobre el sistema.

Para poder determinar las resistencias Ra y Rb que cumplan con las condiciones se usara la relación de transformación (a), el error (Er%) seleccionado y la tensión sobre el equipo (Vvolt) seleccionado.

• Calculo Ra y Rb:

Con el valor de la relación de transformación (a) y la tensión que cae sobre el equipo (Vvolt) se puede calcular el valor de la tensión medida (Vm):

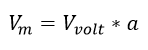
Ecuación 2.3.2.2.10 Calculo tensión medida

Con el valor de la tensión medida (Vm) y la tensión Thevenin (Vth) se determina el valor de la tensión sobre la resistencia Thevenin (VRth) por medio de una ley de tensiones de Kirchhoff:

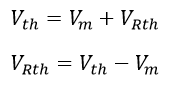
Ecuación 2.3.2.2.11 Calculo tensión VRth

Con la tensión sobre la resistencia Thevenin (VRth) y la resistencia Thevenin (Rth) se puede determinar el valor de la corriente del sistema de medición (Im) por medio de una ley de ohm:

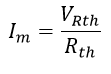
Ecuación 2.3.2.2.12 Calculo Corriente Im

Como la tensión sobre la resistencia Ra (VRa) y el equipo (Vvolt) son componentes de la tensión medida (Vm) se puede determinar el valor de la tensión sobre Ra (VRa):

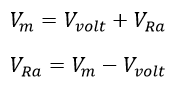
Ecuación 2.3.2.2.13 Calculo tensión VRa

Con esta tensión sobre la resistencia Ra (VRa) y la corriente del sistema (Im) se puede determinar la resistencia Ra por medio de una ley de ohm:

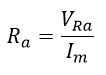
Ecuación 2.3.2.2.14 Calculo resistencia Ra

Una vez obtenido el valor de la resistencia Ra y usando la relación de transformación (a) previamente calculada, se puede determinar una expresión para la resistencia paralelo (Rp):

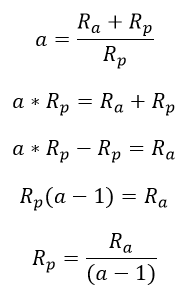
Ecuación 2.3.2.2.15 Calculo resistencia Rp

Ahora que se posee el valor de la resistencia paralelo (Rp) y la resistencia del equipo (Rvolt) es conocida gracias al catálogo, se puede determinar el valor de la resistencia Rb:

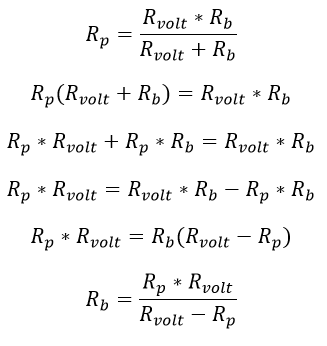
Ecuación 2.3.2.2.16 Calculo resistencia Rb

Con los valores de Ra y Rb es posible determinar la potencia consumida con estas, esto con el fin de realizar la selección en la normalización de datos:

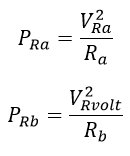
Ecuación 2.3.2.2.17 Potencias Ra y Rb

Una vez obtenido los valores de Ra y Rb (con sus respectivas potencias) se deben llevar a valores reales, de acuerdo a valores dados por fabricantes.

• Normalización de valores y cálculo de incertidumbre

Al ser calculada Ra y Rb se debe encontrar un valor comercial aproximado (ya sea fabricación propia con varias resistencias o una única resistencia) y realizar las correcciones adecuadas al sistema con el nuevo valor de Ra N y Rb N (normalización de los valores), por lo que la incertidumbre de Ra N y Rb N será determinado por un equipo de medición o por la tolerancia que esta pueda poseer (todo depende de lo que sea más exacto y cómodo):

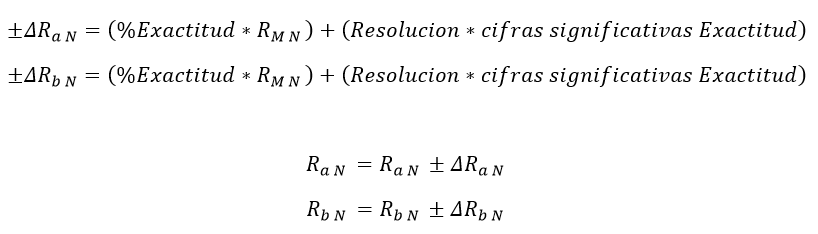
Ecuación 2.3.2.2.18 Incertidumbre Ra y Rb normalizada

Con este valor de Resistencia multiplicadora Rb N se puede calcular el valor de la resistencia paralelo entre Rb N y Rvolt:

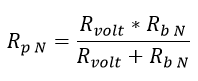
Ecuación 2.3.2.2.19 Resistencia Serie

Ya que la resistencia Rvolt no posee incertidumbre (a menos que el catalogo indique lo contrario) y la incertidumbre de Rb N se encuentra una propagación de la incertidumbre a la resistencia Rp N:

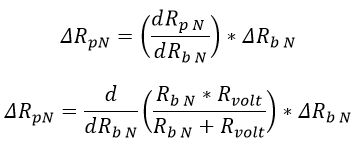
Ecuación 2.3.2.2.20 Calculo incertidumbre Resistencia paralelo

Aunque parezca complicada la derivación se usa la derivación de un cociente recordando que Rb N es el valor variable:

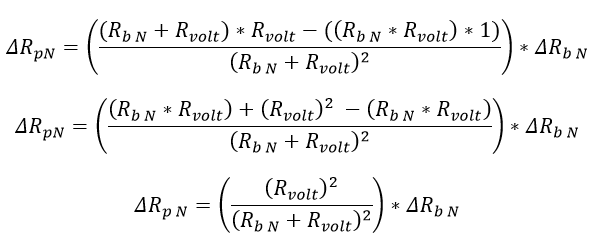
Ecuación 2.3.2.2.21 Incertidumbre Resistencia paralelo normalizada

Con el valor de las resistencias Rp N y Ra N se puede determinar una equivalente serie (Rs N):

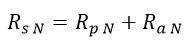
Ecuación 2.3.2.2.22 Resistencia serie normalizada

Debido a que Rp N y Ra N poseen incertidumbre, se puede calcular la propagación de la incertidumbre en una suma de variables para la resistencia Rs N:

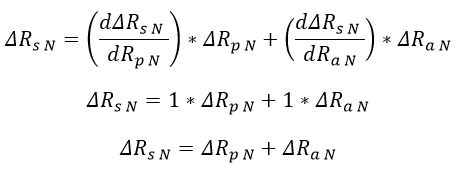
Ecuación 2.3.2.2.23 Incertidumbre Resistencia serie normalizada

Con el valor de la tensión Vth (que es un valor independiente al sistema de medida), y las resistencias Rth y Rs se puede determinar el valor de la corriente del sistema (Im):

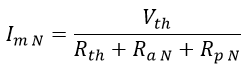
Ecuación 2.3.2.2.24 Corriente medida Normalizada

Con el valor de la corriente del sistema de medida (Im N) y el valor de la resistencia paralelo (Rp N) se puede determinar el valor normalizado de la tensión vista por el equipo (Vvolt N):

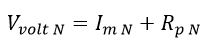
Ecuación 2.3.2.2.25 Tensión Vvolt normalizado

Como la tensión del equipo (Vvolt N) es el valor que va a registrar el equipo, el cálculo de la incertidumbre depende del catálogo:

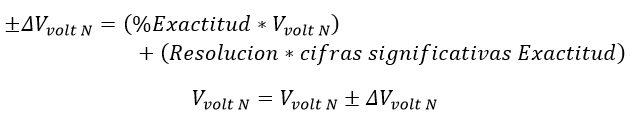
Ecuación 2.3.2.2.26 Incertidumbre Vvolt normalizada

Al igual que la tensión del equipo (Vvolt N) la resistencia Rth es medida por un equipo, es decir su incertidumbre depende del catálogo:

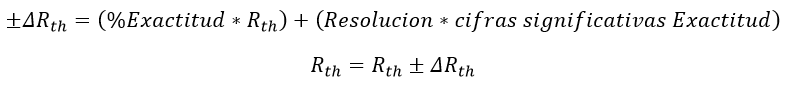
Ecuación 2.3.2.2.27 Incertidumbre Rth

Con las incertidumbres de Vvolt N y Rp N es posible determinar la incertidumbre de la corriente del sistema (Im N) por medio de una división entre incertidumbres de una ley de ohm:

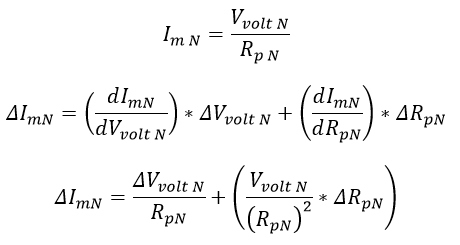
Ecuación 2.3.2.2.28 Incertidumbre Im Normalizada

Con los valores de Im N y Rs N es posible calcular la tensión medida (Vm N):

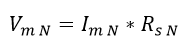
Ecuación 2.3.2.2.29 Tensión Vm Normalizada

Como la corriente Im N y la resistencia Rs N poseen incertidumbre, es posible determinar la incertidumbre de Vm N por medio de la multiplicación entre dos variables:

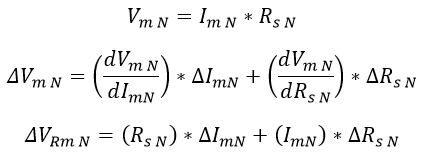
Ecuación 2.3.2.2.30 Incertidumbre Tensión Vm normalizada

Con los valores de Vm N y Vvolt N y sus respectivas incertidumbres, se puede realizar el cálculo de la relación de transformación y su respectiva incertidumbre:

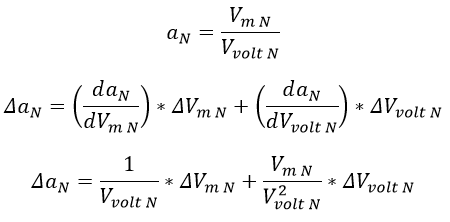
Ecuación 2.3.2.2.31 Valor e incertidumbre de la relación de transformación normalizada

Con los valores de Im N y Rth por medio de una ley de ohm se puede determinar el valor de la tensión que cae sobre la resistencia Thevenin (VRth):

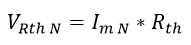
Ecuación 2.3.2.2.32 Tensión VRth Normalizada

Como la corriente Im N y la resistencia Rth poseen incertidumbre, es posible propagar la incertidumbre por medio de la multiplicación entre dos variables para determinar la incertidumbre de la tensión VRth N:

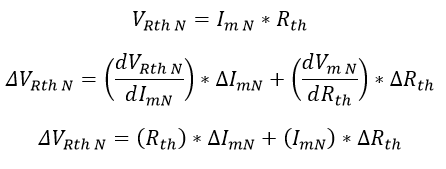
Ecuación 2.3.2.2.33 Incertidumbre tensión VRth Normalizada

Por medio de una ley de tensiones de Kirchhoff es posible propagar la incertidumbre de VRth N y Vm N hacia la tensión Vth:

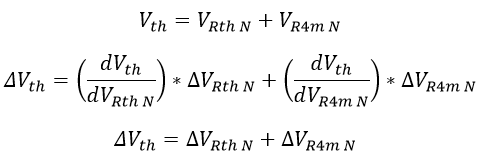
Ecuación 2.3.2.2.34 Calculo Incertidumbre Vth Normalizada

Y así finaliza el cálculo de las principales variables del sistema con normalizaciones e incertidumbres (Vth, Rth, Vm, Ra, Rb, Vvolt, VRth, a), para el cálculo de potencias solo hay que aplicar la ley de ohm de potencia y la propagación de incertidumbre en la multiplicación de dos variables pero con el fin de no alargar el texto esto se deja al análisis del estudiante para cada uno de los casos:

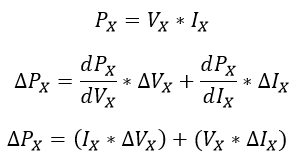
Ecuación 2.3.2.2.35 Calculo de potencia con incertidumbre

Conclusiones:

• Con la medición de Tensión indirecta - Divisor resistivo es posible determinar la tensión vista por el equipo, garantizando una medición segura.

• El análisis de la relación de transformación vista desde el error garantiza errores pequeños según lo desee el operador.

• Al ser Rp una resistencia equivalente de un paralelo no puede exceder el valor de la resistencia del voltímetro ya que como se puede ver se obtiene una resta entre estos (Rvolt - Rp), si Rp es mayor a la resistencia del multímetro se está ignorando la ley de los circuitos paralelos la cual dice que el resultado debe ser menor que las dos resistencias involucradas en la operación (Rb y Rvolt) debido a que la resistencia del multímetro Rvolt ya es conocida gracias al manual del fabricante.

• Debido a la limitación de Rp no es posible realizar un análisis del error visto desde las resistencias, debido a que son bastantes puntos a tener en cuenta, lo que no genera una confiabilidad adecuada y puede llevar a errores de resistencias negativas.

• Si se realiza un análisis del error visto desde las resistencias se ignora el equipo de medición y no se posee control sobre la tensión que cae sobre este, por lo que puede llegar a ser peligroso.

• Debido a su configuración protege al equipo y al operador de este.

 

2.3.2.1 Multiplicadores	3.1 Modelor Real de elementos pasivos de Circuito: Resistencias, Inductores y capacitores