1.7.Transformada de Laplace

1.7.1.Definición, transformadas básicas

1.7.1.1 Definición

Sea f una función en el dominio del tiempo definida para , entonces la Transformada de Laplace asociada se expresa como,

que se entiende como la transformación de la función f con dominio en el tiempo, a una función F con dominio en la frecuencia compleja. La aplicación de esta herramienta a la solución de ecuaciones integro-diferenciales de cualquier orden en circuitos eléctricos en estado transitorio, optimiza la reducción de operaciones complejas para la solución del sistema, trasladando el problema al dominio de la frecuencia donde se realizan procedimientos algebraicos y finalmente con una transformación inversa de Laplace, se traslada dicha respuesta como función en el dominio s, a una función en el dominio del tiempo.

1.7.1.2 Transformadas básicas

Aplicando la definición expresada en la ecuación 5.7.1, se pueden deducir las transformadas de funciones básicas.

1.7.1.2.1 Transformada de una constante

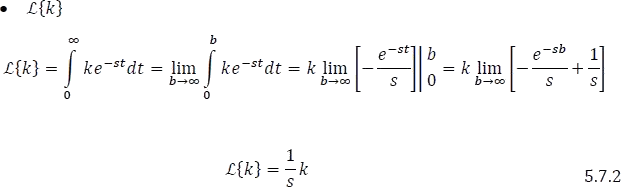
1.7.1.2.2 Transformada de una potencia

1.7.1.2.3 Transformada de una función exponencial

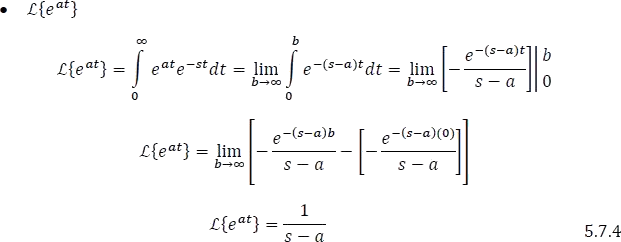
1.7.1.2.4 Transformada de las funciones sinusoidales

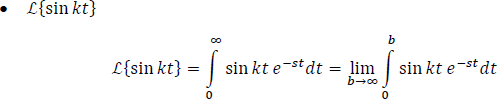
Expresando la función en términos de la Identidad de Euler, se obtiene:

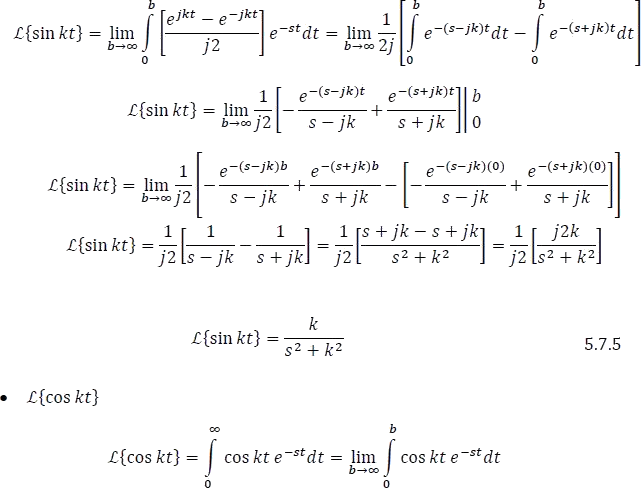
Expresando la función 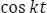en términos de la Identidad de Euler, se obtiene:

1.7.1.2.5 Transformada de algunas funciones hiperbólicas

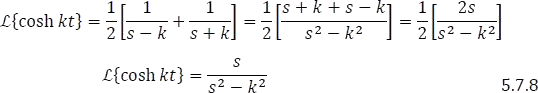
1.7.1.2.6 Transformada de la función Heaviside

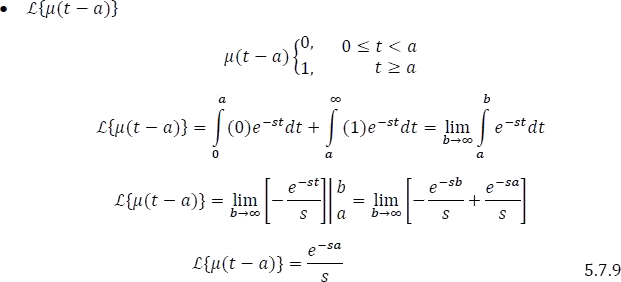
1.7.1.2.7 Transformada de la función Delta de Dirac

A medida que toma la forma 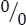, luego se utiliza la regla de L`Hopital

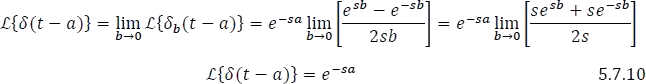
1.7.1.2.8 Transformada de una derivada

La ecuación 5.7.1.1 solo define la transformada de Laplace de como:

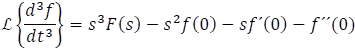
Reorganizando la ecuación 5.7.1.1.

En general,

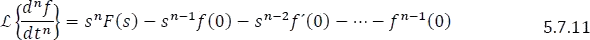
1.7.1.2.9 Transformada de una integral

Sean

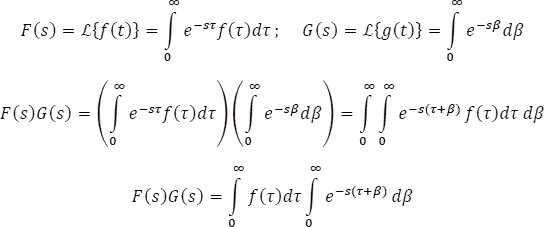
Dejando fijo,hacemos 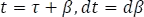y cambiando los límites de integración respectivamente se tiene,

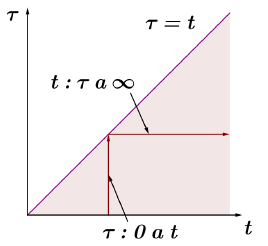
Finalmente,

1.7.1.2.10 Derivada de una transformada

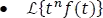
Desarrollando el caso de la primera derivada de una transformada se tiene

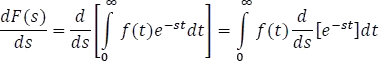
que por definición de transformada de Laplace es

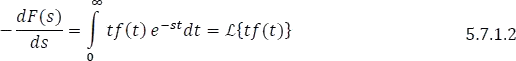
y es la transformada de Laplace para

Ahora desarrollando el caso de la segunda derivada de una transformada se tiene

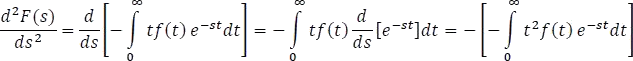
que por definición de transformada de Laplace es

y es la transformada de Laplace para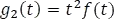

De las ecuaciones 5.7.1.2 y 5.7.1.3 se concluye que:

1.7.1.2.11 Transformada de una función periódica

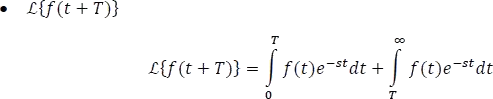
Haciendo la sustitución 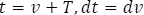, para la integral de la derecha

Sustituyendo en la ecuación principal

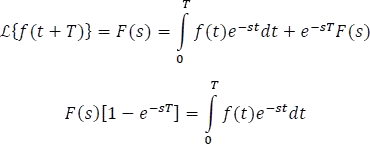
Finalmente,

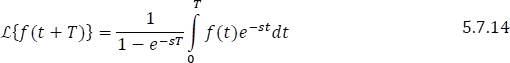
Tabla 5.7.1 Resumen de transformadas de Laplace

 

Respuesta completa ante fuentes distinta a escalón, como senoidales, rampas, polinomiales, combinaciones	Teoremas