1.6.Respuesta completa ante fuentes distinta a escalón, como senoidales, rampas, polinomiales, combinaciones
En el titulo anterior se obtuvo la formula sintética de la respuesta completa. A continuación, se hallarán las formulas sintéticas particulares para las fuentes no constantes más usadas y algunas de sus combinaciones.
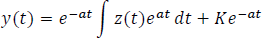
- Respuesta completa a una entrada sinusoidal
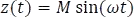
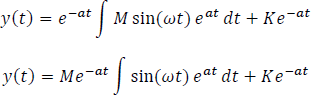
Para resolver la integral 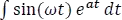 se debe aplicar el método de integral por partes. Dicha integral es cíclica, por lo que se resolverá por aparte.
se debe aplicar el método de integral por partes. Dicha integral es cíclica, por lo que se resolverá por aparte.
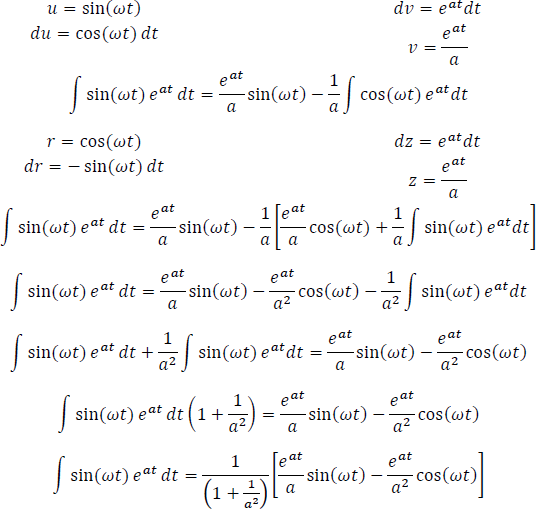
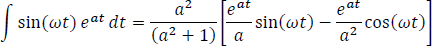
Empalmando la solución anterior a la ecuación de y(t) se obtiene
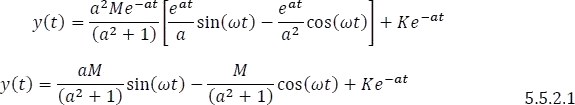
Finalmente, para simplificar mayormente la ecuación 5.5.2.1 se asigna el nombre de -5-6.png) y
y -5-6.png) a las constantes obtenidas. Así, se encuentra la respuesta completa de forma general para una entrada sinusoidal.
a las constantes obtenidas. Así, se encuentra la respuesta completa de forma general para una entrada sinusoidal.
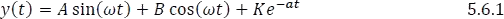
- Respuesta completa a una entrada exponencial
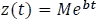

Donde -5-6.png) y
y -5-6.png) una contante J, se tiene
una contante J, se tiene

- Respuesta completa a una entrada tipo rampa
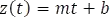
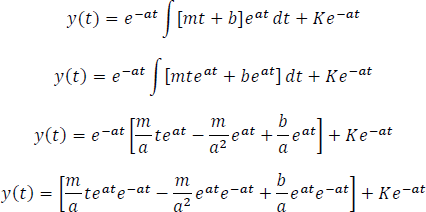

Con 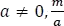 una contante I y
una contante I y 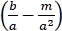 una constante J se tiene,
una constante J se tiene,

- Respuesta completa a una entrada sinusoidal amortiguada

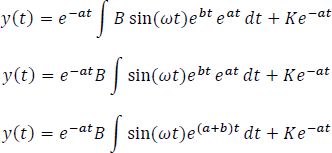
Al igual que se hizo con la solución para la Respuesta completa a una entrada sinusoidal, aquí, hay que aplicar en la integral 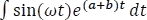 el método de integral por partes. Dicha integral es cíclica, por lo que se resolverá por aparte.
el método de integral por partes. Dicha integral es cíclica, por lo que se resolverá por aparte.
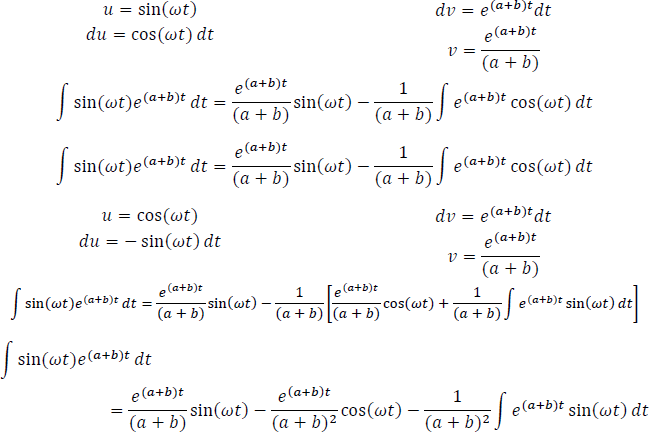
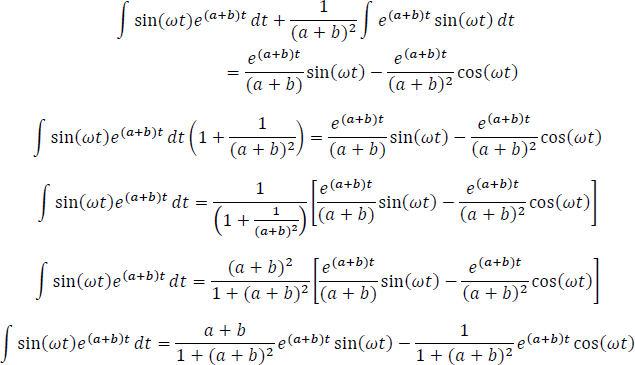
Empalmando la solución anterior, a la ecuación de y(t)
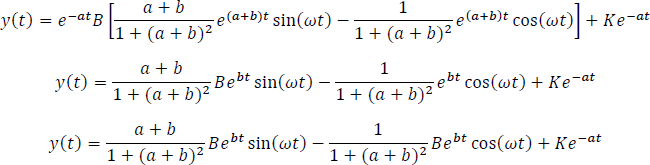
Finalmente, se obtiene la forma general de la respuesta completa para una entrada sinusoidal amortiguada.


Donde 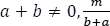 una contante
una contante  una constante I y
una constante I y 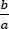 una constante J se tiene:
una constante J se tiene:


|
 |
Determinación de la respuesta natural y forzada de circuito de orden uno |
Transformada de Laplace. Definición, transformadas básicas |
