1.7.2 Teoremas

1.7.2.1 Teorema del valor inicial

Este teorema permite encontrar las condiciones iniciales de un circuito, es decir el comportamiento de f(t) en cuando es continua, pero si f es discontinua en , se deberá encontrar el valor inicial a partir del límite haciendo una aproximación desde tiempos positivos a . Este teorema es válido para señales diferentes a pulsos, delta de dirac o derivadas de la misma en el origen.

El valor inicial de f se puede hallar utilizando

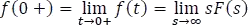
Para demostrar este teorema se usará la propiedad de la transformada de una derivada, como sigue:

Haciendo el límite cuando

Se parte la integral de la ecuación  en dos límites puesto que la función se define convenientemente por partes.

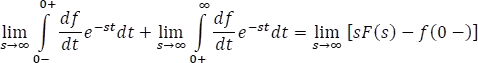
Resolviendo la integral de la izquierda tenemos:

Resolviendo la integral de la derecha:

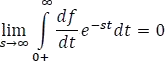
Finalmente,

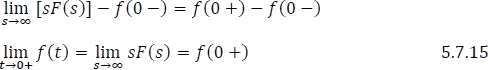
1.7.2.2 Teorema del valor final

Este teorema permite encontrar las condiciones finales de un circuito, es decir el comportamiento de f(t) cuando y es continua.

El valor final de f se puede hallar utilizando

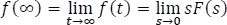
Para demostrar este teorema se usará la propiedad de la transformada de una derivada, como sigue:

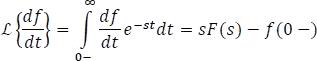
Haciendo el límite cuando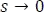

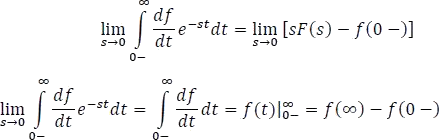
Finalmente,

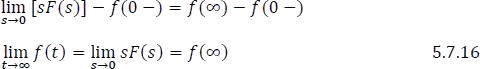
1.7.2.3 Primer teorema de traslación

La transformada de Laplace de una función f multiplicada por una función exponencial de la forma , es decir 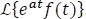, puede hallarse de forma directa conociendo la transformada de f, y trasladándola a .

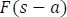El primer teorema de traslación define:

Sea F(s), la transformada de una función f, y a sea un número real, entonces:

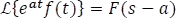
Esta definición se demuestra a partir de la definición 5.7.1, como sigue:

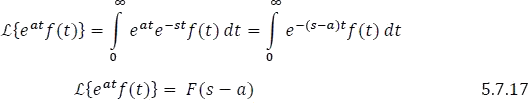
Gráficamente como,

Figura 5.7.2 Traslación de F en el eje s

Y la ecuación 5.7.17 se puede simbolizar como,

1.7.2.4 Segundo teorema de traslación

Así como una función f(t), acompañada de un múltiplo exponencial traslada la trasformada F(s) en el eje s; una consecuencia de ello es que un múltiplo exponencial de F(s), traslade o desplace la transformada inversa, es decir, f(t) a 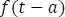, con .

El segundo teorema de traslación define:

Sea F(s), la transformada de una función f, y , entonces:

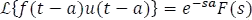
Esta definición se demuestra a partir de la definición 5.7.1, (definición transformada de Laplace) como sigue:

Esta integral puede dividirse en dos integrales ya que se está multiplicando una función escalón, la cual nos deja como resultado una función a trozos

Como la definición de transformada de Laplace exige unos límites de integración de cero hasta infinito, se realiza la sustitución .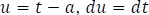

Si , luego los límites de la integral son

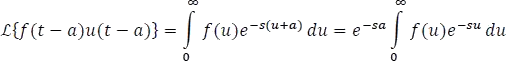
Finalmente,

Gráficamente como,

Figura 5.7.3 Traslación de f en el eje t

1.7.2.5 Teorema de convolución

Un producto especial para f(t) y g(t), si son funciones continuas a trozos en 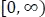, se define por la integral,

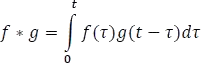
que se llama convolución de f y g, que da como resultado una función en el dominio del tiempo.

El teorema de convolución define:

Si f(t) y g(t) son funciones continuas a trozos en, 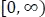y de orden exponencial entonces,

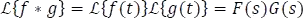
Demostración:

Sean

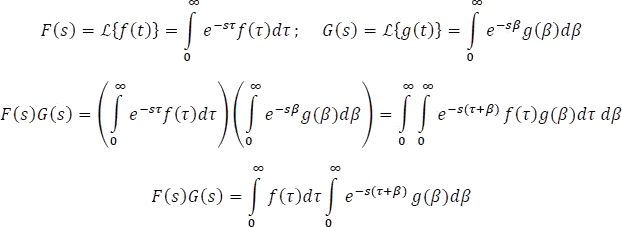
Dejando Τ fijo, hacemos y cambiando los límites de integración respectivamente, Figura 5.7.1, se tiene

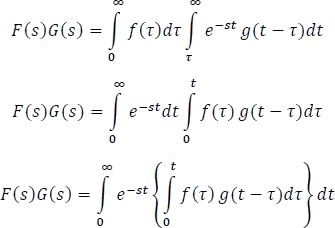
Finalmente,

 

Transformada de Laplace. Definición, transformadas básicas.	Fracciones parciales