1.7.3 Fracciones parciales

Es de suma importancia saber descomponer una función racional ya sea propia o impropia en fracciones parciales con el fin de determinar en el caso de Laplace, la transformada inversa, es decir, la respuesta en el tiempo de un determinado sistema en estado transitorio, donde se encontrarán casos en la transformación de ecuaciones diferenciales por medio de la definición 5.7.1 como los que se describirán más adelante. La función en el dominio de la frecuencia a la cual se le dará este tratamiento es de la forma:

Donde A(s) es el numerador y B(s) es el denominador de la función racional.

1.7.3.1 Fracciones propias

Una fracción racional propia es aquella que está compuesta por la división de dos polinomios, en la cual el grado (n) del polinomio del numerador, es menor al grado (m) del polinomio del denominador, tal como lo presenta la ecuación 5.7.20.

Ejemplo:

A continuación, se presentan diferentes casos de este tipo de función racional.

1.7.3.1.1 Denominador con factores lineales diferentes

Una fracción racional con factores lineales, es aquella en la que su denominador es un polinomio, que al ser factorizado se obtendrá uno o varios factores de la forma 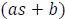, donde a y b son números reales.

Para poder expandir una función racional en fracciones parciales, se deben seguir los siguientes pasos:

• Factorizar completamente B(s) en factores lineales de la forma .

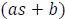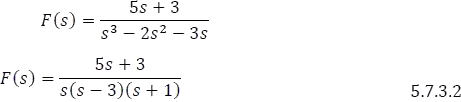
• Asignar a cada factor lineal una constante A, B, C o D según la cantidad de factores.

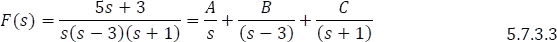
• Multiplicar a ambos lados de la ecuación 5.7.3.3 por y simplificar.

• Identificar el valor en el cual cada factor se vuelve cero o fijar un valor para s.

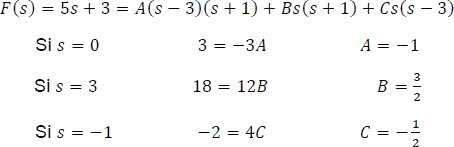
• Aplicar la transformada inversa de Laplace a cada término de la ecuación 5.7.3.4., así:

• Finalmente, encontrar la función en el dominio del tiempo

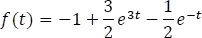
1.7.3.1.2 Denominador con factores lineales repetidos

Cuando se habla de factores lineales repetidos se piensa en una expresión de la forma , donde a y b son números reales y k es un numero entero positivo mayor o igual a 2.

Ejemplo:

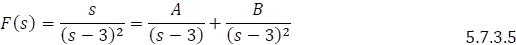
• Multiplicar a ambos lados de la ecuación 5.7.3.5. por y simplificar.

• Identificar el valor en el cual cada factor se vuelve cero o fijar un valor para s y encontrar los coeficientes.

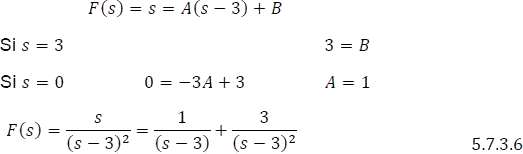
• Aplicar la transformada inversa de Laplace a la ecuación 5.7.3.6, así:

Como se observa en las dos fracciones de la ecuación 5.7.3.7, no es posible hacer la transformada inversa de Laplace de forma directa, por lo que es propio usar el primer teorema de translación definido en la ecuación 5.7.17 y con la ayuda de la Tabla 5.7.1, se tiene:

• Finalmente, encontrar la función en el dominio del tiempo

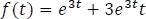
1.7.3.1.3 Denominador con raíces complejas y distintas

Se dice que una función racional tiene en su denominador un polinomio con coeficientes reales y raíces complejas, cuando dicho polinomio no tiene solución en el conjunto de los números reales.

Ejemplo:

• Asignar al factor cuadrático irreducible de la ecuación 5.7.3.8 el término .

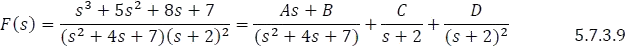
• Multiplicar a ambos lados de la ecuación 5.7.3.9 por 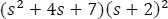, simplificar y encontrar los coeficientes.

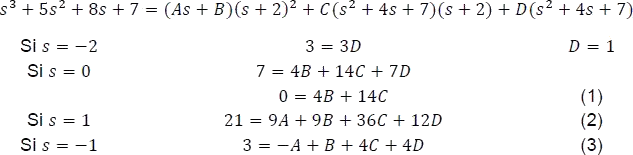
• Multiplicando la ecuación (3) por 9 y aplicar el método de reducción entre las ecuaciones (2) y (3)

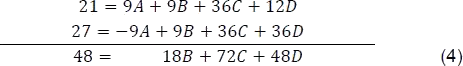
• Reemplazando en la ecuación (4), 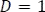queda

• Multiplicando la ecuación (5) por 4 y reduciendo con la ecuación (1)

• Reemplazando en la ecuación (3)

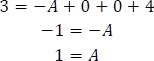
• Luego, la fracción quedaría expandida así:

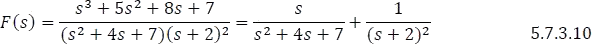
Ahora, para poder aplicar la transformada inversa de Laplace, primero se debe factorizar del denominador de la ecuación 5.7.3.10 completando cuadrados.

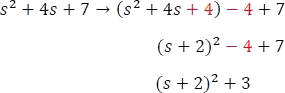
La mitad del coeficiente de 4s es 2, 2 se eleva al cuadrado lo que resulta ser un 4, que se sumará y restará en la ecuación, con el fin de no afectarla, luego los tres primeros términos se vuelven un trinomio cuadrado perfecto que se puede factorizar en un binomio al cuadrado.

• Habiendo echo lo anterior, la nueva función será

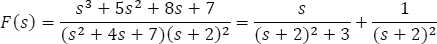
Lo siguiente, será asemejar el numerador del primer término al denominador del mismo, sin alterar la fracción.

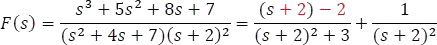
Pues bien, ahora según el primer teorema de traslación 5.7.17, será sustituido por s y 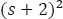se reemplazará por

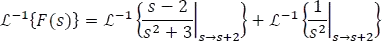
Separando algebraicamente las transformadas

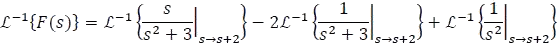
Luego, siguiendo Tabla 5.7.1 se percibe que el segundo término necesita tener 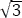en el numerador, por lo que se multiplicará y dividirá por dicho número, de esta forma se podrá hallar la transformada inversa de Laplace.

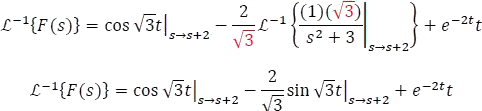
Racionalizando 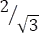se tiene,

Finalmente, encontrando la función en el dominio del tiempo

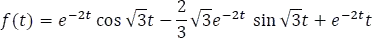
1.7.3.2 Fracciones impropias

Una fracción racional impropia es aquella que está compuesta por la división de dos polinomios, en la cual el grado (n) del polinomio del numerador es mayor o igual al grado (m) del polinomio del denominador, tal como lo presenta la ecuación 5.7.20.

Una función racional de este tipo tiene la forma,

Siendo el cociente, R(s) el residuo, A(s) el dividendo y B(s) el divisor de la división algebraica.

Cuando se está frente a este tipo de funciones racionales, antes de aplicar el método de fracciones parciales, se debe hacer una división algebraica o sintética entre el numerador y el denominador, y luego proseguir con la aplicación del método si es necesario.

Ejemplo:

• Realizar una división algebraica

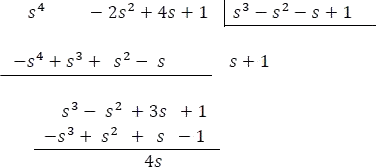
• Organizar el resultado de la división algebraica que es equivalente a la fracción inicial dada.

De lo obtenido en la ecuación 5.7.3.11, se identifican tres términos, dos de los cuales permiten hallar la transformada inversa de Laplace de forma directa; pero al término tres, se le aplicará el método de fracciones parciales así:

• La función completa quedaría así:

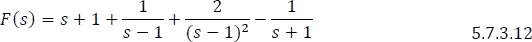
• Aplicando la transformada inversa de Laplace a la ecuación 5.7.3.12, se tiene:

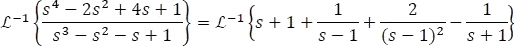
Para hallar la transformada inversa de Laplace de las tres fracciones resultantes, se utilizará el primer teorema de traslación 5.7.17. Para este caso se tiene:

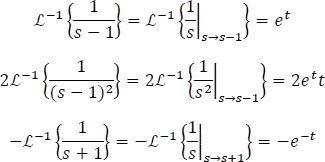
Finalmente, la respuesta completa en el dominio del tiempo es:

 

Teoremas	Solución de una ecuación diferencial utilizando transformada de Laplace, con y sin condiciones iniciales, para circuitos de orden uno, concepto de ganancia y constante de tiempo