1.7.4 Solución de una ecuación diferencial utilizando transformada de Laplace, con y sin condiciones iniciales para circuitos de orden uno, concepto de ganancia y constante de tiempo.

La transformada de Laplace aplicada a la solución de los circuitos de orden uno se podrá ver en muchos casos. Aquí se mostrarán algunos ejemplos.

1.7.4.1 Circuito sin condiciones iniciales o condiciones cero.

Sean 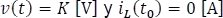. Halle y para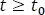

Figura 5.7.4 Circuito R-L sin condiciones iniciales.

Como las condiciones iniciales son nulas, entonces no se analiza el circuito en tiempos menores a .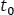

Aplicando LVK al circuito anterior se tiene:

Reescribiendo la ecuación 5.7.4.1

Ahora aplicando la transformada de Laplace a la ecuación diferencial 5.7.4.2 usando las propiedades de la Tabla 5.7.1 Resumen de transformadas de Laplace, se tiene:

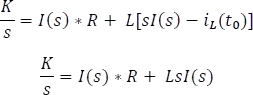
Factorizando y despejando I(s)

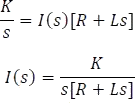
Aplicando fracciones parciales

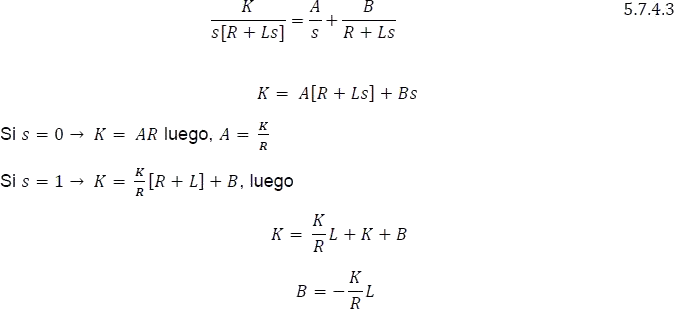
Reemplazando los coeficientes A y B en la ecuación 5.7.4.3

Multiplicando el término 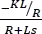por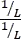

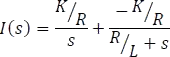
Aplicando transformada inversa de Laplace

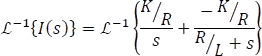
Como el tiempo de cierre del interruptor es en un tiempo cualquiera , entonces la respuesta correcta para la corriente es:

Figura 5.7.5 Respuesta de la corriente en la bobina.

Ahora hallando a partir de la respuesta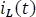

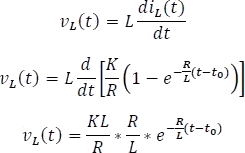
Finalmente,

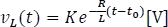
Figura 5.7.6 Respuesta de la tensión en la bobina.

Para recordar: La inductancia L no permite cambios bruscos de corriente, entonces se comporta como un circuito abierto un instante después de que se conmuta el interruptor en 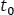, en donde su voltaje será igual a la tensión impuesta por la fuente de alimentación.

1.7.4.2 Circuito con condiciones iniciales.

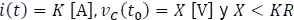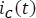Sean . Halle e para

Figura 5.7.7 Circuito R-C con condiciones iniciales.

Aplicando LCK en el nodo de conexión de R, se tiene

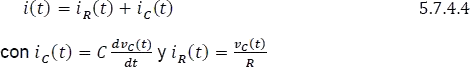
Reescribiendo la ecuación 5.7.4.4

Ahora aplicando la transformada de Laplace a la ecuación diferencial 5.7.4.5 usando las propiedades de la Tabla 5.7.1 Resumen de transformadas de Laplace.

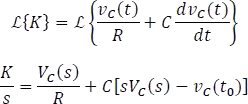
Factorizando y despejando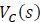

Multiplicando el término por se obtiene

Aplicando fracciones parciales al primer término de la suma se tiene

Reemplazando los coeficientes A y B en la ecuación 5.7.4.7

Multiplicando el término por

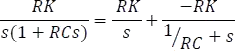
Reescribiendo la ecuación 5.7.4.6

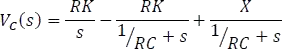
Aplicando transformada inversa de Laplace

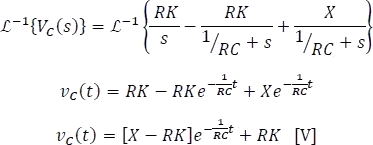
Como el tiempo de cierre del interruptor es en un tiempo cualquiera 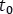, entonces la respuesta correcta para la tensión es:

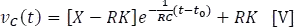
Figura 5.7.8 Respuesta de la tensión en el condensador.

Ahora hallando 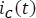a partir de la respuesta

Finalmente,

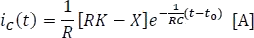
Figura 5.7.9 Respuesta de la corriente en el condensador.

1.7.4.3 Concepto de ganancia

La ganancia puede definirse como una magnitud adimensional que representa a nivel de los circuitos eléctricos y/o electrónicos la relación que existe entre una señal de entrada y una señal de salida que generalmente puede encontrarse para saber valores de tensión, corriente y potencia a la salida de un determinado circuito que este mismo puede cambiar para una aplicación específica.

 

Fracciones parciales	Definición de función de transferencia, respuesta a estados cero y respuesta a fuentes cero, fuentes impulso, escalón, caja unitaria, senoidales, polinomiales, combinaciones