1.7.5. Definición de función de transferencia, respuesta a estados cero y respuesta a fuentes cero, fuentes impulso, escalón, caja unitaria, senoidales, polinomiales, combinaciones

1.7.5.1 Función de transferencia

Una función de transferencia es la relación que existe entre una señal de salida y una de entrada, que a su vez permite hallar la respuesta de un sistema frente a un determinado tipo de señal de entrada transfiriéndola a una señal de salida consecuencia de la alteración y/o modificación de dicha señal a través del sistema.

La función de transferencia H(s), (en el dominio de la frecuencia compleja), es matemáticamente, el cociente entre una señal de salida Y(s) y una señal de entrada X(s), siempre y cuando las condiciones iniciales sean nulas. Por tanto,

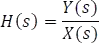
Dentro de las funciones de transferencia que se pueden encontrar comúnmente dentro de los circuitos eléctricos se tienen:

1.7.5.2 Respuesta general a los diferentes estados y entradas

Como se vio en la sección (respuesta completa fórmula sintética), se dedujo una ecuación general o ecuación sintética a partir de la ecuación diferencial general de un circuito de primer orden, resolviéndola por el método de factor integrante; que permitió dejar la respuesta completa en función de la entrada o fuente de alimentación. Ahora se demostrará que a partir de la teoría de La Transformada de Laplace se puede llegar a una ecuación equivalente de la respuesta en función del tiempo, a partir de la ecuación diferencial general de un circuito equivalente RL o RC como sigue,

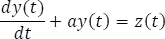
Aplicando la transformada de Laplace a ambos lados de la ecuación se obtiene

Factorizando y despejando Y(s)

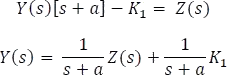
Por último, aplicando la transformada inversa de Laplace a ambos lados de la ecuación

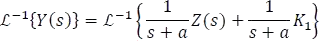
Finalmente,

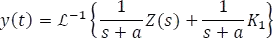
Aquí se obtuvo la ecuación general o fórmula sintética que relaciona la respuesta completa y(t) en función de una entrada de alimentación Z(s) de un circuito de primer orden.

1.7.5.2.1 Respuesta a estado cero o condiciones iniciales cero

Partiendo de la ecuación general de un circuito de primer orden y aplicando la transformada de Laplace a ambos lados de la ecuación se obtiene

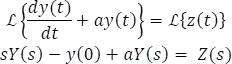
Como se pretende hallar la respuesta a estado cero se tiene que:

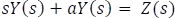
Finalmente,

1.7.5.2.2 Respuesta a fuente cero

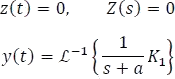
Finalmente, la respuesta a una fuente nula, con condiciones iniciales diferentes de cero es:

1.7.5.2.3 Respuesta a fuente escalón

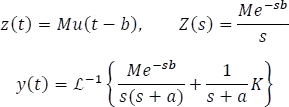
Expandiendo el término en fracciones parciales se tiene:

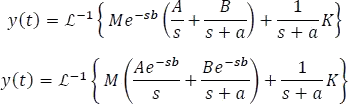
Aplicando el segundo teorema de traslación o traslación en el eje t

Finalmente, la respuesta a una fuente escalón será:

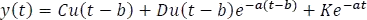
Si 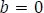y se obtendrá la respuesta al escalón unitario como:

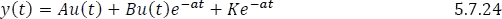
1.7.5.2.4 Respuesta a fuente impulso

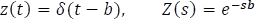
Aplicando el segundo teorema de traslación o traslación en el eje t

Se obtiene la respuesta ante una entrada impulso unitario.

1.7.5.2.5 Respuesta a fuente senoidal

Expandiendo la fracción 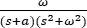en fracciones parciales se tiene:

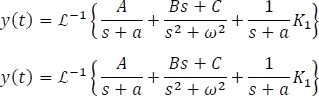
Factorizando 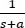y reescribiendo la expresión

Multiplicando 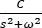por se tiene

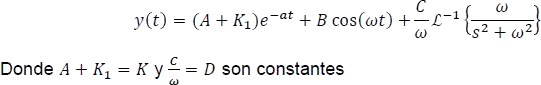
Finalmente, se obtiene la respuesta ante una fuente sinusoidal.

1.7.5.2.6 Respuesta a fuente polinomial

Expandiendo la expresión en fracciones parciales se tiene:

Factorizando y reescribiendo la expresión

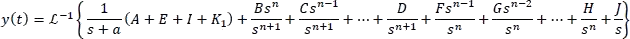
Simplificando la expresión donde 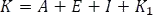y agrupando términos

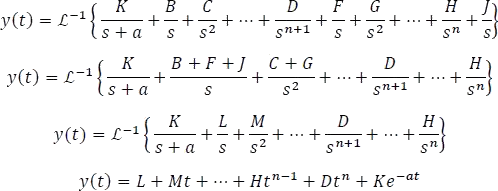
Finalmente, se obtiene la respuesta ante una entrada de tipo polinomial.

 

Solución de una ecuación diferencial utilizando transformada de Laplace, con y sin condiciones iniciales, para circuitos de orden uno, concepto de ganancia y constante de tiempo	Contenido