1.2.1 Señal escalón unitario e impulso unitario.

1.2.1.1 Escalón unitario

El escalón unitario es una función definida a trozos en donde se muestra el cambio repentino que ocurre en un tiempo específico 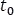, donde en tiempos menores a ese valor la función es nula y en tiempos mayores es la unidad y se modela así:

Figura 5.2.4 Gráfica de la función escalón unitario.

Ejemplo 1: Función escalón

a. Graficar la siguiente función

Como la señal de tensión es un escalón, está es cero cuando el argumento , y es uno cuando el argumento , entonces se definen los valores de t que corresponden a cada intervalo de la función así:

Por último, se define la función a trozos y su gráfica respectiva así:

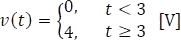
Figura 5.2.5 Señal de tensión para el ejemplo 1, literal a.

b. Graficar la siguiente función

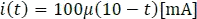
Como la señal de corriente es un escalón que es cero cuando el argumento 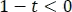, y es uno cuando el argumento 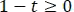, entonces se definen los valores de t que corresponden a cada intervalo de la señal así:

Por último, se define la función a trozos y su gráfica respectiva así:

Figura 5.2.6 Señal de corriente para el ejemplo 1, literal b.

1.2.1.1.1 Operaciones con la función escalón

Ejemplo 2: Suma de una constante con una función escalón

• Hallar la función resultante gráficamente.

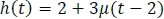
Luego, se define la función a trozos y su gráfica respectiva así:

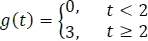
Figura 5.2.7 Gráfica g(t) para el ejemplo 2.

Haciendo gráficamente se obtiene:

Figura 5.2.8 Suma de las funciones f(t) y g(t).

En el intervalo de 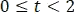se tiene la suma de y en el siguiente intervalo de se tiene la suma de 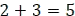. Por consiguiente, la gráfica resultante es:

Figura 5.2.9 Gráfica resultante para el ejemplo 2.

Ejemplo 3: Suma de funciones escalón

• Hallar la función resultante gráficamente

Se define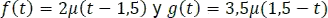

Luego, se define la función a trozos y su gráfica respectiva así:

Figura 5.2.10 Gráfica f(t) para el ejemplo 3.

Para :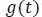

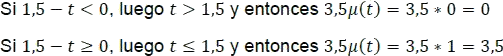
Luego, se define la función a trozos y su gráfica respectiva así:

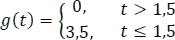
Figura 5.2.11 Gráfica g(t) para el ejemplo 3.

Haciendo , gráficamente se tiene:

Figura 5.2.12 Suma gráfica de las funciones f(t) y g(t).

En el intervalo de 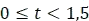se tiene la suma de 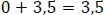y en el siguiente intervalo de se tiene la suma de 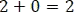. Por consiguiente, la gráfica resultante es:

Figura 5.2.13 Gráfica resultante para el ejemplo 3.

Ejemplo 4: Producto de funciones escalón

• Sea y 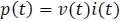la potencia disipada por una resistencia, halle la función producto gráficamente.

Luego, se define la función a trozos y su gráfica respectiva así:

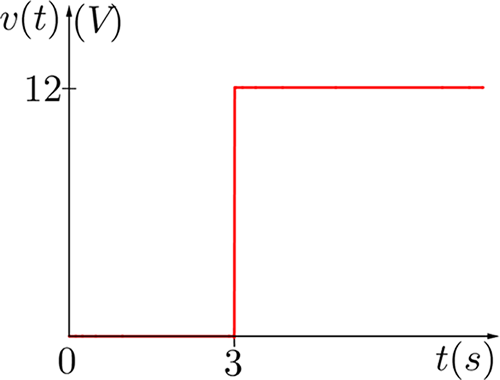
Figura 5.2.14 Señal de tensión para el ejemplo 4.

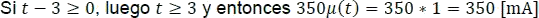
Luego, se define la función a trozos y su gráfica respectiva así:

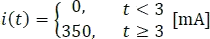
Figura 5.2.15 Señal de corriente para el ejemplo 4.

Haciendo el producto gráficamente se obtiene,

Figura 5.2.16 Producto gráfico entre las señales de tensión y corriente.

En el intervalo de 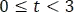segundos, se tiene el producto de y en el siguiente intervalo de 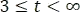segundos, se tiene el producto de . Por consiguiente, la gráfica resultante es:

Figura 5.2.17 Señal de potencia resultante para el ejemplo 4.

Del ejemplo 4 se concluye que:

En general,

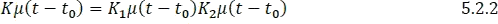
Donde 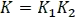y son constantes.

Ejemplo 5: Producto de funciones escalón

• Sea . Halle la función producto gráficamente.

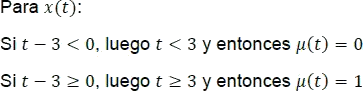
Luego, se define la función a trozos y su gráfica respectiva así:

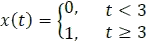
Figura 5.2.18 Gráfica x(t) para el ejemplo 5.

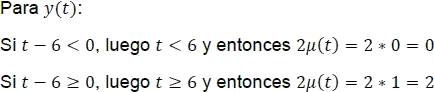
Luego, se define la función a trozos y su gráfica respectiva así:

Figura 5.2.19 Gráfica g(t) para el ejemplo 5.

Haciendo el producto gráficamente,

Figura 5.2.20 Producto gráfico entre las funciones x(t) y y(t).

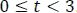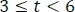En el intervalo de , se tiene el producto de , en el siguiente intervalo de , se tiene el producto de y en el intervalo de 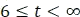, se tiene el producto . Por consiguiente, la gráfica resultante es:

Figura 5.2.21 Gráfica resultante del producto x(t)y(t).

Del ejemplo 5 se concluye que:

En general,

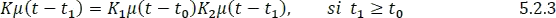
Donde 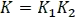y son contantes

1.2.1.2 Impulso unitario

El impulso unitario es una función definida a trozos, que se obtiene por la suma o multiplicación de dos escalones unitarios, que pueden ser de voltaje o de corriente. Tiene como característica, que su área bajo la curva es unitaria y que tiene una duración de . Por lo que,

Figura 5.2.22 Señal impulso unitario.

Demostración gráfica.

Este impulso puede construirse a partir del producto o suma de dos funciones escalón. A continuación, se muestra la construcción a partir del producto de dos funciones escalón, como sigue,

Figura 5.2.23 Producto gráfico entre funciones escalón.

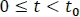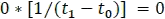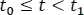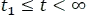En el intervalo de , se tiene el producto de , en el siguiente intervalo de , se tiene el producto de y en el intervalo de , se tiene el producto . Luego:

 

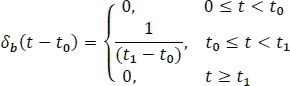
Evaluación de las condiciones iniciales en circuitos con L y C, ante fuentes constantes	Circuitos con interruptores o fuentes dependientes, señales escalón