1.4. Respuesta natural

La respuesta natural, es una solución general de la ecuación diferencial que modela el comportamiento de una variable de circuito cuando en este no se encuentra presente una fuente de alimentación que fuerce su respuesta.

1.4.1. Determinación de la ecuación característica de circuitos de orden uno, sin fuentes.

1.4.1.1 Respuesta natural para un circuito RL

A partir de la ecuación diferencial para circuitos de orden uno sin fuentes, hallada en el título anterior, se llega a la ecuación característica para los mismos circuitos, por lo que se procede a encontrar usando el método de variables separables, con el cual integraremos a ambos lados de la ecuación 5.3.1:

Primero despejar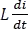

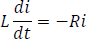
Luego, multiplicar por dt a ambos lados

Multiplicar a ambos lados por 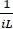con el fin de dejar los términos que tienen i a un lado, junto con el diferencial de corriente.

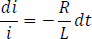
Integrar a ambos lados de la ecuación, usando como límites la condición inicial 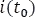, y la corriente que habrá en el elemento cuando se abre el interruptor, es decir , que será la condición en . También se reemplazarán las variables t e i por x y y correspondientemente.

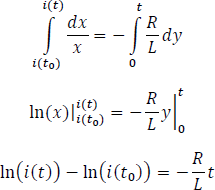
Por propiedades de los logaritmos, el logaritmo de una resta es igual al logaritmo de un cociente

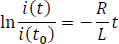
Multiplicando a ambos lados por la expresión Euler se puede despejar .

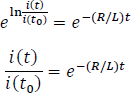
Finalmente, se obtendrá la respuesta natural

1.4.1.2 Constante Tau para un circuito RL

La constante de tiempo tau 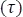(para este caso particular), es el tiempo que transcurre cuando un inductor comienza a perder la carga que había obtenido de una fuente directa a la cual estaba conectada anteriormente, entonces, cuando pasa un tau o una constante de tiempo, el porcentaje de corriente que estará circulando por el inductor será de 36,8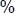, es decir, este elemento habrá entregado un 63,2 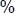de su corriente inicial, y así sucesivamente hasta que sucedan 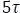, que será donde la bobina se habrá descargado totalmente. Así se observa en la Tabla 5.4.1.

El tau también nos indica la velocidad de descarga en segundos, por lo que a menor tau mayor será su velocidad de descarga y a mayor tau más lenta será su descarga.

Tabla 5.4.1Porcentajes de descarga en un elemento almacenador de energía según el tau.

Ahora se mostrará como hallar la ecuación del tau para un circuito RL.

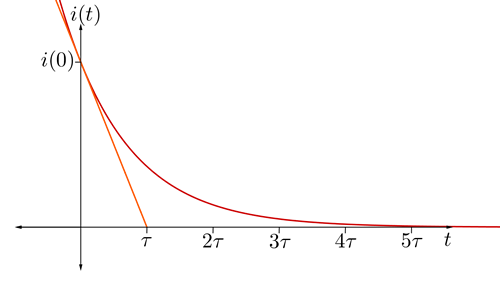
Figura 5.4.1Respuesta de corriente del inductor en un circuito R-L sin fuentes.

1. Hallar la pendiente de la recta tangente en .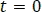

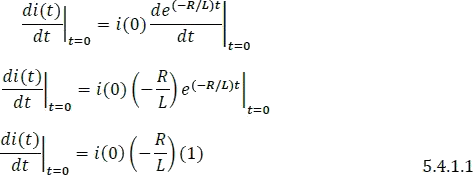
2. Hallar la pendiente de la misma recta usando la ecuación de pendiente.

3. Igualar las ecuaciones 5.4.1.1 y 5.4.1.2 despejando tau.

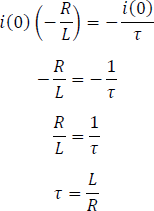
La unidad del tau será en segundos. Con esto, la ecuación característica en un circuito RL, ecuación 5.4.1 se podrá representar como:

Ejemplo:

Del circuito de la Figura 5.4.2 halle para , suponiendo que el interruptor estuvo por mucho tiempo cerrado y se abrirá en . (Charles K. Alexander, 2006, pág. 226)

Figura 5.4.2 Ejemplo circuito R-L mixto.

Para : como el interruptor lleva mucho tiempo cerrado, en el instante 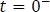, el inductor actúa como un cortocircuito, este comportamiento también dejara en cortocircuito a la resistencia . Entonces el circuito resultante será:

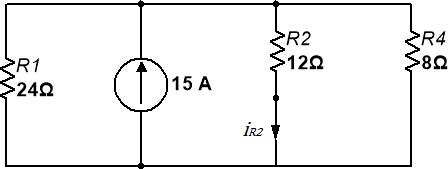
Figura 5.4.3 Circuito resultante para analizar en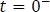

Haciendo un paralelo entre las resistencias 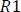y 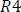se obtiene:

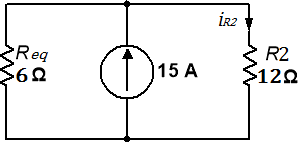
Figura 5.4.4 Circuito equivalente.

Luego, para el circuito de la Figura 5.4.4 se encontrará la condición en 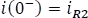con ayuda de un divisor de corriente.

Para : teniendo en cuenta que el inductor no admite cambios bruscos, la condición inicial 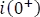será igual a la corriente en .

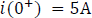
Para : para este tiempo, el interruptor se vuelve a abrir, dejando desconectada la fuente de corriente y la resistencia 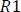, por lo que ahora se tendrá un circuito RL sin fuente con una resistencia equivalente, como se muestra en la Figura 5.4.5.

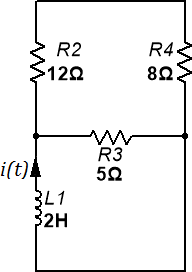
Figura 5.4.5 Circuito resultante para analizar en .

Haciendo un paralelo entre la resistencia serie 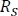y se calculará la resistencia total, con la cual se encontrará el tau.

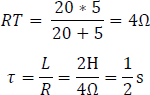
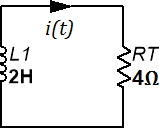
Figura 5.4.6 Circuito R-L sin fuente resultante.

De esta forma, la ecuación diferencial representativa para este circuito es:

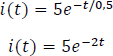
1.4.1.3 Respuesta natural para un circuito RC

A partir de la ecuación diferencial para circuitos de orden uno sin fuentes, se llega a la ecuación característica para los mismos circuitos, por lo que se procede a encontrar 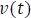usando el método de variables separables, con el cual integraremos a ambos lados de la ecuación 5.3.2:

Primero despejar

Luego, multiplicar por 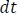a ambos lados

Multiplicar a ambos lados por con el fin de dejar los términos que tienen v a un lado, junto con el diferencial de corriente.

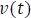Integrar a ambos lados de la ecuación, usando como límites la condición inicial y la tensión que habrá en el elemento cuando se abre el interruptor, es decir , que será la condición en . También se reemplazarán las variables t y v por x y y correspondientemente.

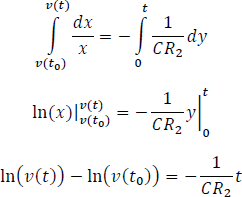
Por propiedades de los logaritmos, el logaritmo de una resta es igual al logaritmo de un cociente.

Multiplicando a ambos lados por la expresión Euler se puede despejar .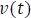

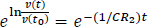
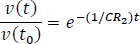
Finalmente, se obtendrá la respuesta natural

De la ecuación 5.4.2, se puede observar, que la respuesta de la tensión en el condensador se comporta como una disminución exponencial de la tensión inicial.

1.4.1.4 Constante Tau para un circuito RC

La constante de tiempo tau (para este caso particular), es el tiempo que transcurre cuando un condensador comienza a perder la carga que había obtenido de una fuente constante a la cual estaba conectada anteriormente, entonces, cuando pasa un tau o una constante de tiempo, el porcentaje de tensión que estará circulando por el inductor será de 36,8, es decir, este elemento habrá entregado un 63,2 de su tensión inicial, y así sucesivamente hasta que sucedan 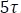, que será donde el capacitor se habrá descargado totalmente. Así se observa en la Tabla 5.4.2.

El tau también nos indica la velocidad de descarga en segundos, por lo que a menor tau mayor será su velocidad de descarga y a mayor tau más lenta será su descarga.

Tabla 5.4.2 Porcentajes de descarga en un condensador según el tau.

Ahora se mostrará como hallar la ecuación del tau para un circuito RC.

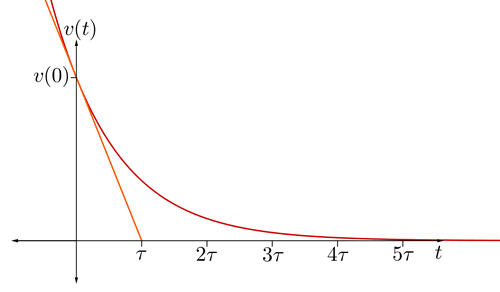
Figura 5.4.7 Respuesta de tensión del condensador en un circuito RC sin fuentes.

1. Hallar la pendiente de la recta tangente en

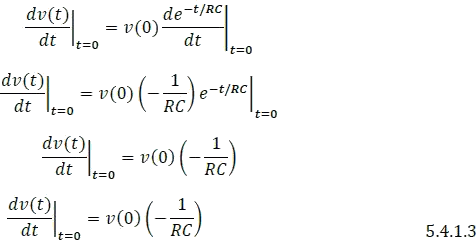
2. Hallar la pendiente de la misma recta usando la ecuación de pendiente.

3. Igualar las ecuaciones 5.4.1.3 y 5.4.1.4 y despejar tau.

La unidad del tau será en segundos. Con esto, la ecuación característica en un circuito RC se podrá representar como:

Ejemplo:

Encontrar para y la energía en el condensador para el siguiente circuito, teniendo en cuenta que el interruptor se abre en .

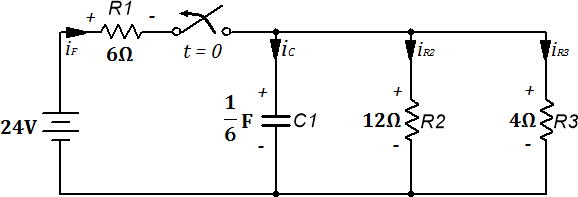
Figura 5.4.8 Ejemplo circuito RC mixto.

Para 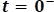: considerando que el interruptor dura mucho tiempo cerrado, en el instante el circuito se verá como el de la Figura 5.4.9.

Figura 5.4.9 Circuito RC resultante para

Para este momento, se puede encontrar 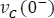. Primero, se hará un equivalente entre las resistencias 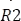y 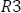, luego se encontrará la corriente del circuito y posteriormente hallará la tensión .

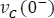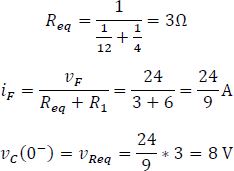
Para : teniendo en cuenta que el condensador no admite cambios bruscos, la condición inicial será igual a la tensión en .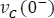

Para : para este tiempo, el circuito se reducirá al de la Figura 5.4.10

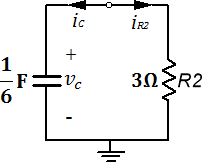
Figura 5.4.10 Circuito RC sin fuente para .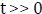

el cual se analizará para construir la ecuación diferencial característica. Por esto, es necesario calcular el tau del circuito de la siguiente forma.

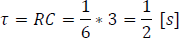
Luego, aplicando la ecuación 5.4.3, se obtendrá la respuesta natural de un circuito RC sin fuentes, .

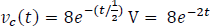
Finalmente, como el ejercicio solicita la energía en el condensador se calculará como sigue:

 

Obtención del modelo de un parámetro, a partir de la ecuación diferencial en otro elemento.	Respuesta completa