1.3.3. Obtención del modelo de un parámetro, a partir de la ecuación diferencial en otro elemento

Para este caso, se encontrará una ecuación diferencial general expresada en función del tiempo, que modele un parámetro de circuito en un elemento, partiendo de la ecuación diferencial típica de corriente o tensión de un condensador o de un inductor, también, usando las leyes básicas y los métodos de solución de circuitos. Como se ilustra en los siguientes casos.

Cabe aclarar que el objetivo de hacer estas demostraciones o estos modelamientos de forma general para circuitos particulares obedece a querer exponerle al estudiante, que se pueden resolver circuitos rápidamente, cuando uno de los valores inicialmente planteados en el ejercicio propuesto, sea cambiado por otro valor numérico, entonces, sólo será reemplazar en la ecuación encontrada el nuevo valor.

1.3.3.1 Circuitos RL

1. Hallar el parámetro en la resistencia a partir de la ecuación típica de tensión en el inductor .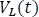

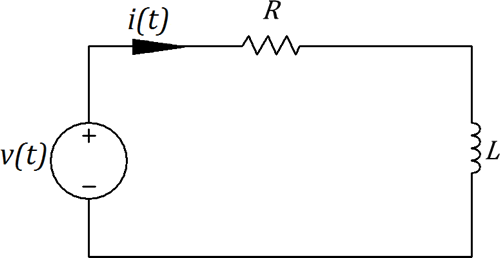
Figura 5.3.9 Circuito RL para el ejemplo 1.

Despejando 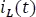de .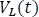

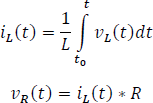
Haciendo sumatoria de tensiones en el lazo cerrado.

Reemplazando tensiones por corrientes.

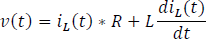
Dividiendo por L a ambos lados de la ecuación.

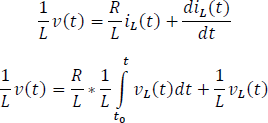
Dejando la expresión en términos de la derivada.

Despejando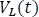

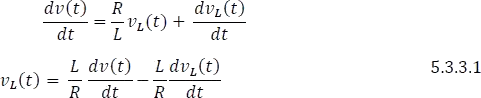
Partiendo de que la derivada de una resta es la resta de sus derivadas, se tiene.

Reemplazando la ecuación 5.3.3.2 en la ecuación 5.3.3.1

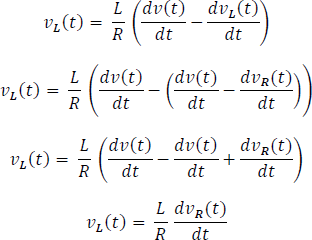
Finalmente encontramos el parámetro a partir de 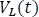o con respecto a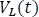

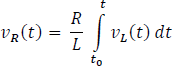
2. Hallar la tensión en la resistencia uno 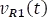a partir de la corriente en la bobina .

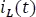Figura 5.3.10 Circuito R-L para el ejemplo 2.

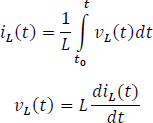
Haciendo una sumatoria de tensiones.

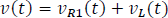
La tensión en la resistencia dos y en la bobina es la misma por lo que podemos decir que:

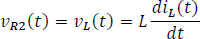
Sumatoria de corrientes en el nodo a

Reemplazando las corrientes por tensiones de acuerdo a la ley de ohm.

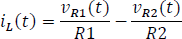
Dejando la ecuación en términos de la corriente en la bobina.

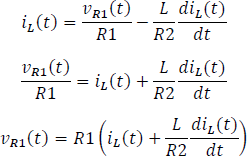
3. Hallar el parámetro 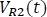en la resistencia a partir de la corriente en la bobina .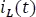

Figura 5.3.11 Circuito R-L para el ejemplo 3.

Se observa que la corriente que pasa por la bobina es la misma que recorre la resistencia 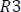, por lo que es posible igualar dichas expresiones así:

Haciendo una sumatoria de tensiones en los dos lazos cerrados podemos despejar la tensión de la resistencia 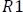e igualar las ecuaciones 5.3.3.5 y 5.3.3.6.

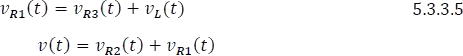
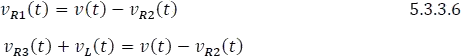
Luego, se reemplaza en la ecuación 5.3.3.7 las expresiones 5.3.3.3 y 5.3.3.4, obteniendo el modelo de 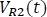en términos de 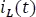, teniendo en cuenta que 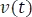en este caso será una constante.

1.3.3.2 Circuitos RC

1. Hallar el parámetro 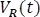en la resistencia a partir de la ecuación típica de tensión en el condensador .

Figura 5.3.12 Circuito R-C para el ejemplo 1.

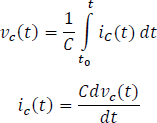
Haciendo una sumatoria de tensiones en el circuito de la Figura 5.3.12.

Reemplazando la tensión de la resistencia en términos de la corriente del condensador, se tiene.

Luego, se encuentra que la ecuación 5.3.3.8 es posible igualarla con la ecuación 5.3.3.9, y así resolver el ejercicio, logrando encontrar el modelo de la tensión en la resistencia en términos de la tensión en el condensador, así:

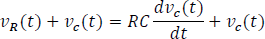
Finalmente,

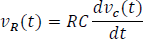
2. Hallar la tensión en la resistencia uno 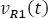a partir de la corriente en el capacitor .

Figura 5.3.13 Circuito R-C para el ejemplo 2.

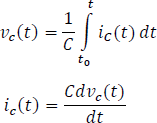
Realizando una sumatoria de corrientes en el nodo a

Reemplazando las ecuaciones 5.3.3.11 y 5.3.3.12 en la ecuación 5.3.3.10 y organizando los términos obtenemos el siguiente modelo.

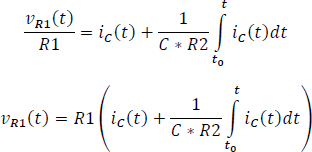
3. Hallar el parámetro 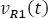en la resistencia a partir de la ecuación típica de tensión en el condensador .

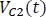Figura 5.3.14 Circuito R-C para el ejemplo 3.

La corriente en el condensador dos es:

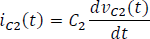
Luego,

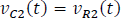
Aplicando LCK en el nodo de conexión del condensador dos, se tiene

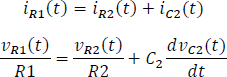
Finalmente, se obtiene el modelo solicitado.

 

Determinación de la ecuación diferencial que describe la relación entre una fuente de entrada y un parámetro de circuito de salida.	Respuesta natural. Determinación de la ecuación característica de circuitos de orden uno, sin fuentes