2.7.2 Aplicación en circuitos

El hecho de poder expresar cualquier señal periódica en términos de sumas de funciones sinusoidales puras es una herramienta muy poderosa a usar en la solución y análisis de circuitos, debido a que es posible hallar la serie de Fourier de la señal de alimentación de un circuito, luego descomponer dicha serie y calcular las respuestas individuales de tensión y corriente para cada termino.

Supongamos que la fuente de alimentación del circuito de la Figura 2.7.1 es periódica no sinusoidal, y su representación en serie de Fourier es la siguiente:

Figura 2.7.1 Circuito lineal alimentado por una señal periódica no sinusoidal

Entonces, se puede descomponer la serie en dos componentes: la primera es su componente DC, y la segunda es una suma de funciones senoidales de diferente amplitud y frecuencia, esta representación se muestra en la Figura 2.7.2.

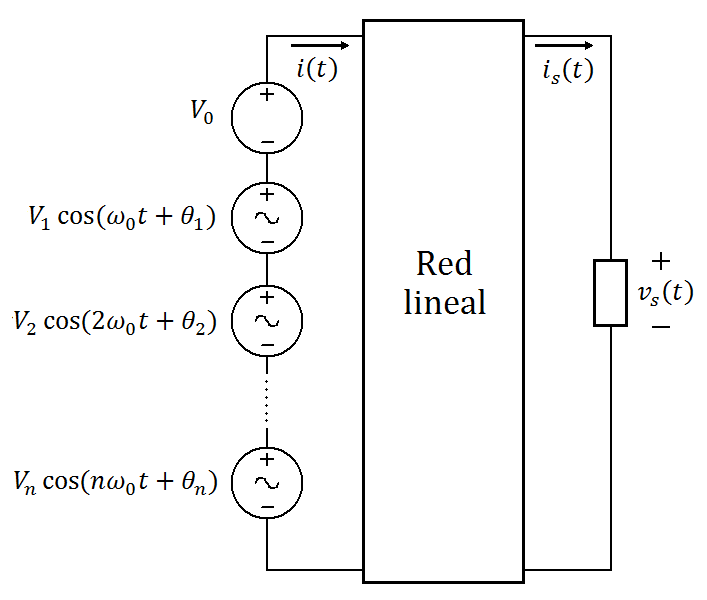
Figura 2.7.2 Representación de la serie de Fourier

Ahora, se usa el teorema de superposición para calcular la respuesta de tensión y corriente del circuito para cada uno de los terminos individuales de la serie, se soluciona cada circuito con los métodos conocidos para corriente directa o corriente alterna, luego se expresa la respuesta en el dominio del tiempo de ser el caso y al final se suman las respuestas individuales para obtener la respuesta total del circuito. Para nuestro caso:

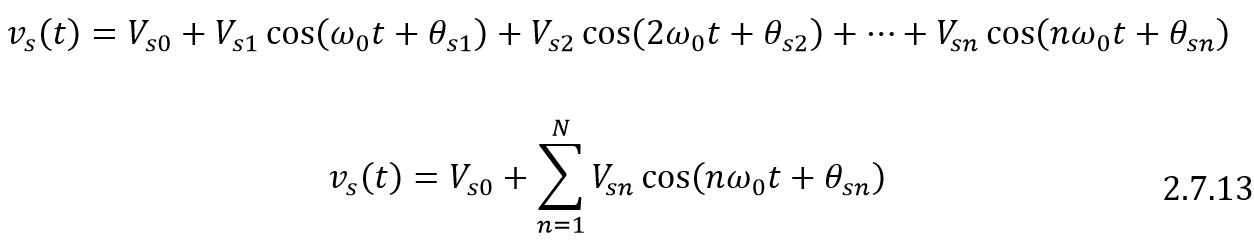
Si se tiene una fuente de corriente se sigue el mismo procedimiento, teniendo en cuenta que las fuentes de corriente deben estar en paralelo.

Serie de Fourier	Valor eficaz de tensión y corriente