2.7 Voltaje, corriente y potencia en circuitos alimentados con señalesperiódicas continuas no sinusoidales

2.7.1 Serie de Fourier

Las series de Fourier reciben el nombre debido a Jean Baptise Joseph Fourier, quien establece que una función periódica no sinusoidal se puede representar como la suma de funciones sinusoidales puras de diferente amplitud y frecuencia.
Entiéndase como una función periódica aquella que se repite cada 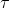segundos, escrito matemáticamente:

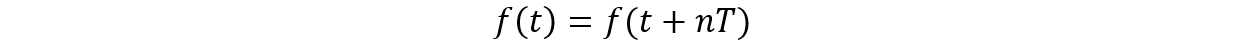
Según el teorema de Fourier, esta función periódica puede representarse como:

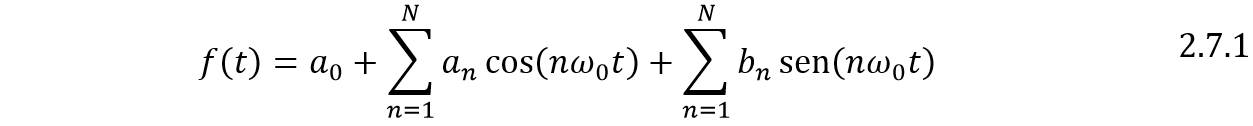
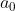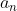Donde   recibe el nombre de frecuencia fundamental ,  y 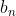 reciben el nombre de coeficientes de Fourier, que se calculan de la siguiente manera:

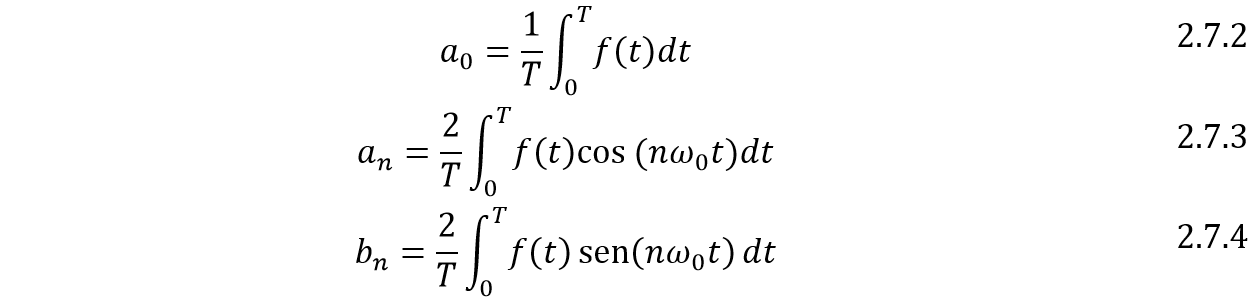
Una representación alternativa de la serie es:

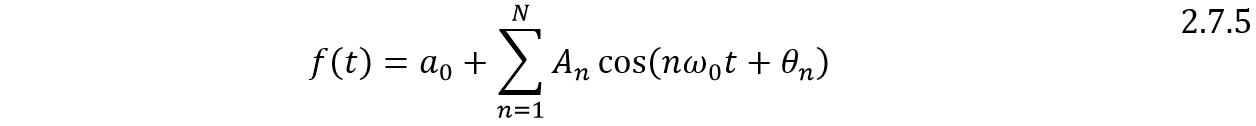
Donde:

Para que una función pueda representarse mediante la serie trigonométrica de Fourier debe cumplir los siguientes requerimientos (Sadiku & Alexander, 2006, pág. 757):

1. Que    sea univoca, es decir que contenga una único valor para cada tiempo.
2.   para cualquier tiempo.
3.   tiene un número finito de discontinuidades finitas en cualquier periodo.
4.   tiene un número finito de máximos y mínimos en cualquier periodo.

Además, si la función que se quiera expresar como serie de Fourier tiene simetría par o impar provoca que se simplifiquen considerablemente los cálculos, como lo veremos inmediatamente.

 

Simetría de función par:

A continuación se examinará que les ocurre a los coeficientes de la serie de Fourier si la función que se quiere tratar es de simetría par, esto quiere decir que , los valores que toma la función para valores de positivos, son los mismos que valores de negativos. (Ejemplo: función coseno)

Para :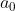

Al ser una función periódica se puede reescribir el intervalo de integración:

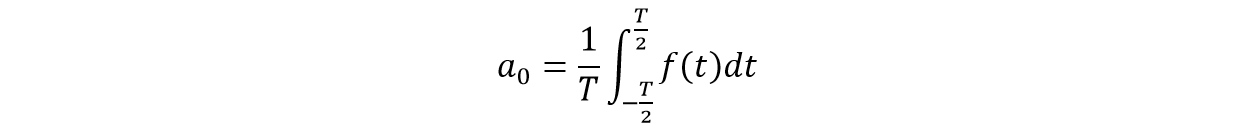
Como la función es de simetría par se puede analizar para medio periodo de tiempo y multiplicando por 2 la integral:

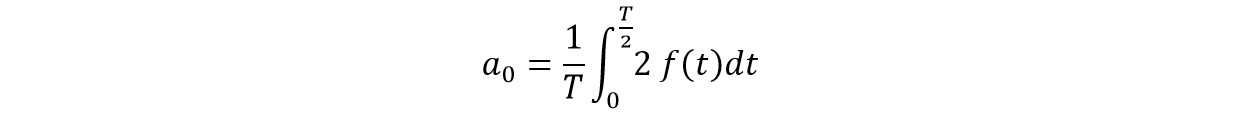
Reorganizando:

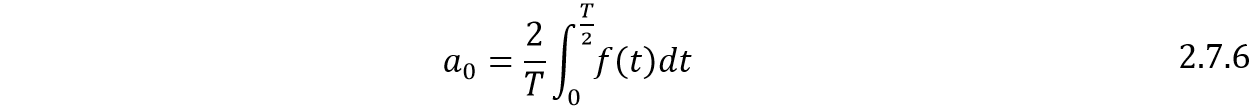
Para :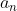

Al ser una función periódica se puede reescribir el intervalo de integración:

Separando la integral en dos intervalos:

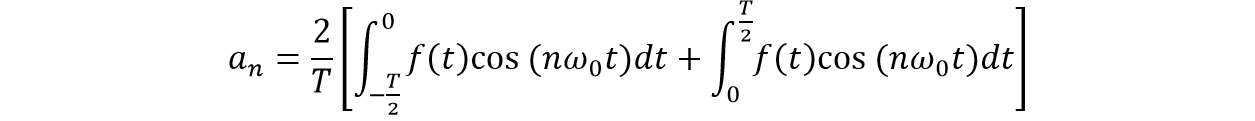
Se quiere dejar ambas integrales con los mismos intervalos, entonces:

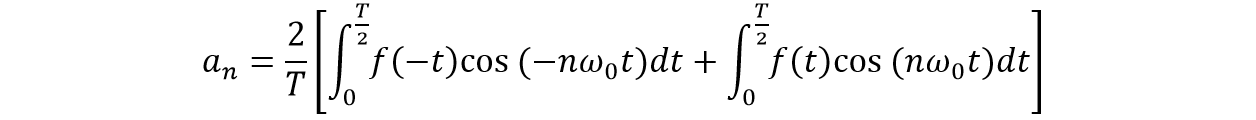
Aplicando la propiedad de función par , para la función a tratar y para el coseno:

Las dos integrales son iguales, entonces:

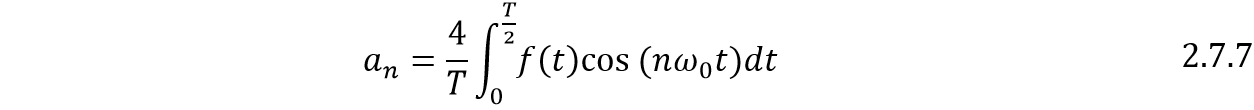
Para :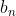

Al ser una función periódica se puede reescribir el intervalo de integración:

Separando la integral en dos intervalos:

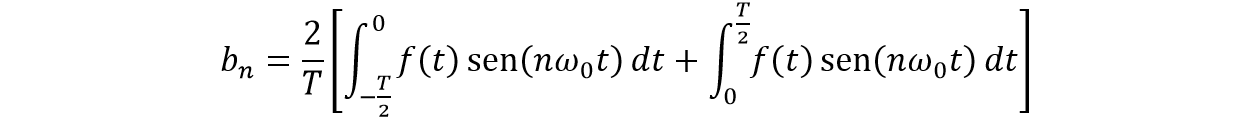
Se quiere dejar ambas integrales con los mismos intervalos, entonces:

Aplicando la propiedad de función par , solo para la función a tratar, mientras que, debido a que la función seno es de simetría impar se aplica ésta propiedad para ella :

Las dos integrales se cancelan:

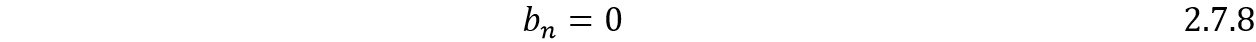
Simetría de función impar:

Ahora se examinará que les ocurre a los coeficientes de la serie de Fourier si la función que se quiere tratar es de simetría impar, esto quiere decir que , los valores que toma la función para valores de negativos, son el valor negativo de valores de positivos. (Ejemplo: función seno).

Para :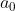

Al ser una función periódica se puede reescribir el intervalo de integración:

Como la función es de simetría impar y al realizar la integral, su valor en el intervalo de a 0 se cancela con su valor en el intervalo de a 0:

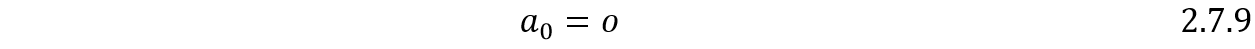
Para :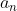

Al ser una función periódica se puede reescribir el intervalo de integración:

Separando la integral en dos intervalos:

Se quiere dejar ambas integrales con los mismos intervalos, entonces:

Aplicando la propiedad de función impar , para la función a tratar y para la función coseno se aplica la propiedad de función par :

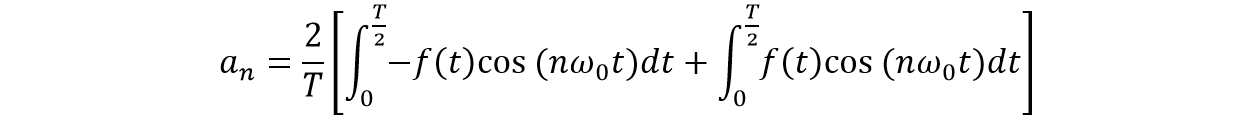
Las dos integrales se cancelan:

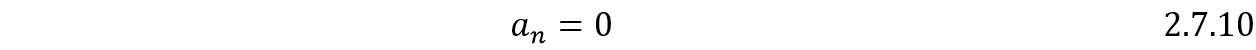
Para :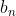

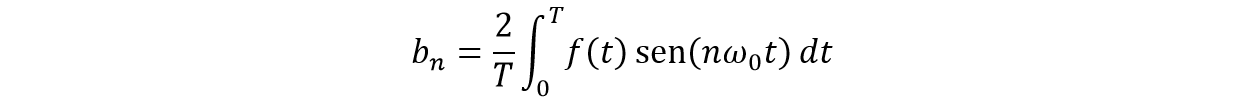
Al ser una función periódica se puede reescribir el intervalo de integración:

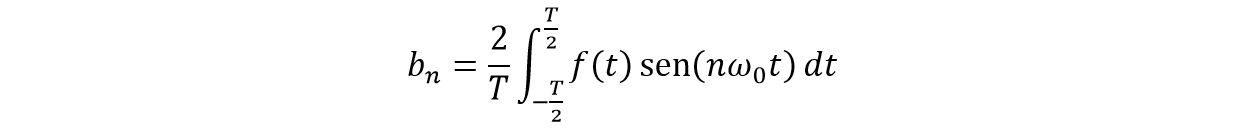
Separando la integral en dos intervalos:

Se quiere dejar ambas integrales con los mismos intervalos, entonces:

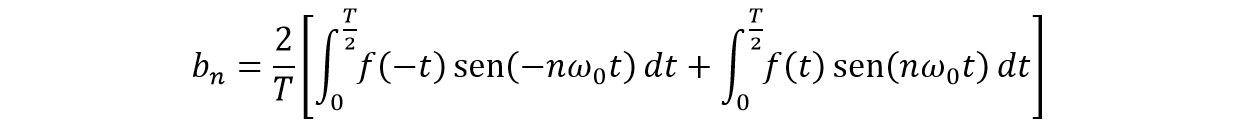
Aplicando la propiedad de función impar para la función a tratar y para la función seno:

Las dos integrales son iguales, entonces:

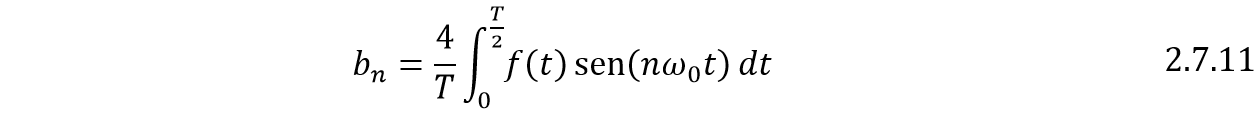
Máxima transferencia de potencia media	Aplicación en circuitos