4.2.2 Método de Aron o de los dos elementos

El método de medición de Aron o de los dos elementos es utilizado en circuitos trifásicos con cargas balanceadas y desbalanceadas, con conexión en delta y en estrella sin neutro. El principio de operación del sistema consiste en que la bobina de tensión del vatímetro mide la tensión de línea y así mismo la bobina de corriente del vatímetro mide la corriente de línea; de esta manera los dos vatímetros deben ser conectados correctamente a dos fases.

La suma algebraica de la lectura de los dos vatímetros es igual a la potencia activa total consumida por la carga.

El método de medición de Aron o de los dos elementos permite realizar tres formas posibles de conexión, dependiendo de su punto de referencia.

A continuación, se analiza un circuito en conexión estrella, el cual sirve como circuito de estudio para realizar el análisis de cada una de las formas de conexión del método de Aron.

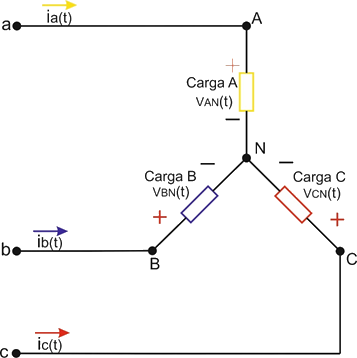
Figura 4.2.5 Circuito para realizar análisis del método de Aron.

Las tensiones de fase se expresan como:

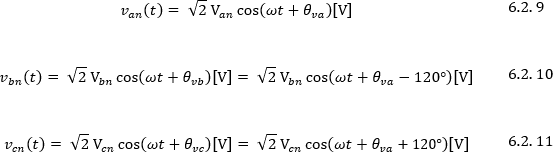
Las corrientes de línea se pueden expresar como:

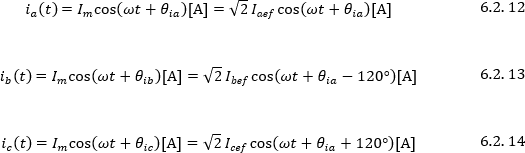
De esta manera la potencia instantánea trifásica del circuito de la Figura 4.2.5 Circuito para realizar análisis del método de Aron será:

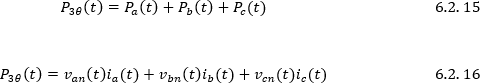
Así la potencia activa trifásica es:

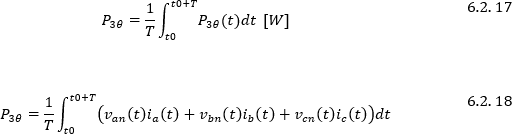
Aplicando LCK para el nodo n se tiene que:

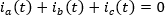
Por lo tanto:

4.2.2.1 Primera forma de conexión del método de los 2 elementos o de Aron, utilizando la fase a como referencia.

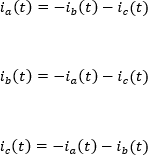
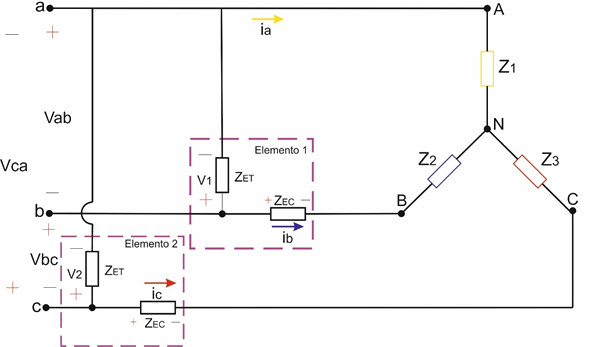
Figura 4.2.6 Método de Aron primera forma de conexión, fase a de referencia.

Reemplazando la corriente 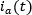en la ecuación de la potencia instantánea para la primera forma de conexión se tiene:

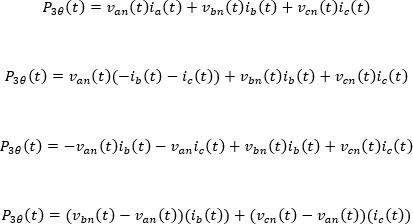
Por lo tanto, la potencia activa trifásica se determina como

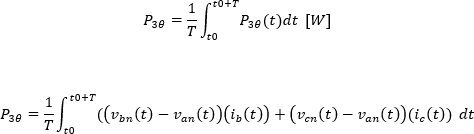
Sustituyendo las ecuaciones de tensión y corriente para cada fase en la ecuación de potencia definida para la fase a se tiene que:

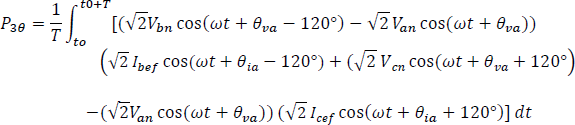
Observemos que en la ecuación anterior se tiene una resta de las tensiones de fase lo cual da como resultado la tensión de línea, a continuación, se realiza dicha operación

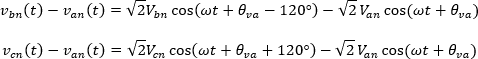
En su forma fasorial se tiene que:

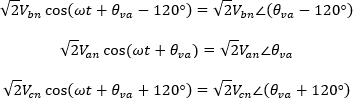
Realizando la resta de tensiones en su forma fasorial:

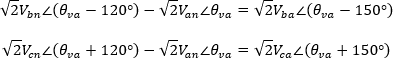
Pasando las ecuaciones del dominio de la frecuencia al dominio del tiempo tenemos:

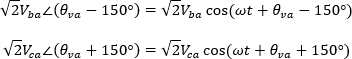
Así la potencia activa se puede expresar como:

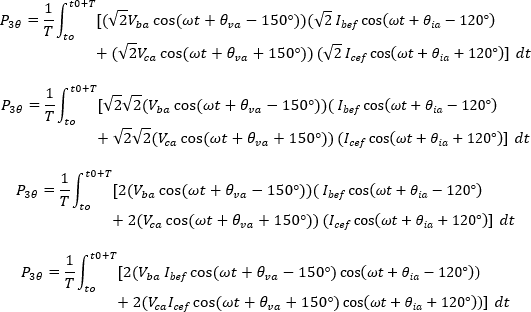
Aplicando la identidad trigonométrica 6.1.5 se tiene:

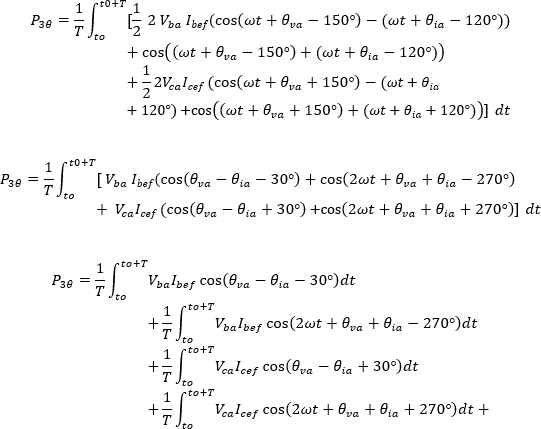
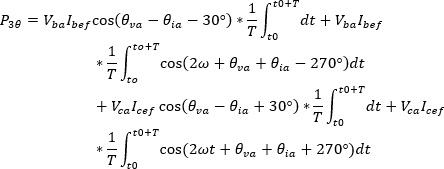
El primer término de la integral para cada vatímetro es independiente del tiempo, por lo tanto, es una constante de la integración.

La segunda integral da como resultado cero, ya que el valor promedio de una onda sinusoidal en un periodo completo es cero; por lo tanto, el segundo término en la ecuación desaparece y la potencia activa trifásica equivale a:

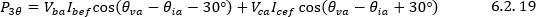
Luego

4.2.2.2 Segunda forma de conexión del método de los 2 elementos o de Aron, utilizando la fase b como referencia.

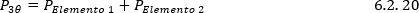
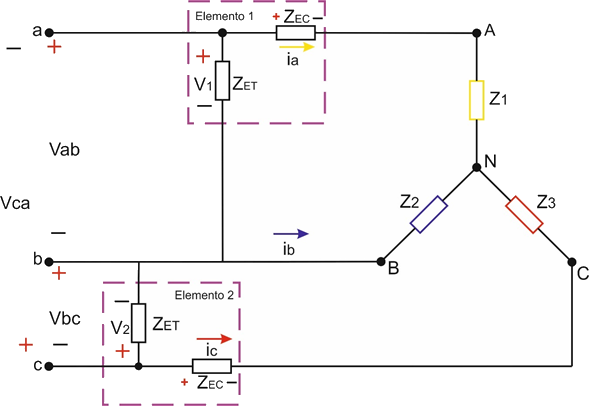
Figura 4.2.7 Método de Aron segunda forma de conexión, fase b de referencia.

Si se reemplaza la corriente 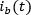en la ecuación de la potencia instantánea para la segunda forma de conexión se tiene:

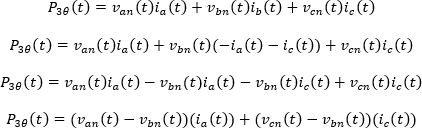
Por lo tanto la potencia activa trifásica se determina como

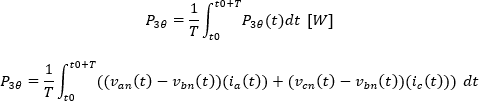
Sustituyendo las ecuaciones de tensión y corriente para cada fase en la ecuación de potencia definida para la fase b se tiene que:

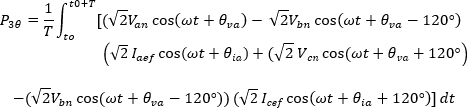
Observemos que en la ecuación anterior se tiene una resta de las tensiones de fase lo cual da como resultado la tensión de línea, a continuación, se realiza dicha operación

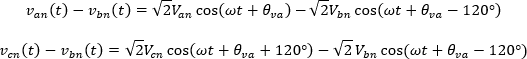
En su forma fasorial se tiene que:

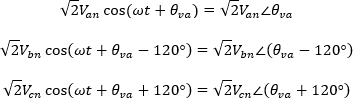
Realizando la resta de tensiones en su forma fasorial:

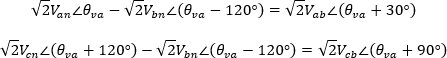
Pasando las ecuaciones del dominio de la frecuencia al dominio del tiempo tenemos:

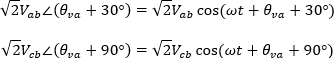
Así la potencia activa se puede expresar como:

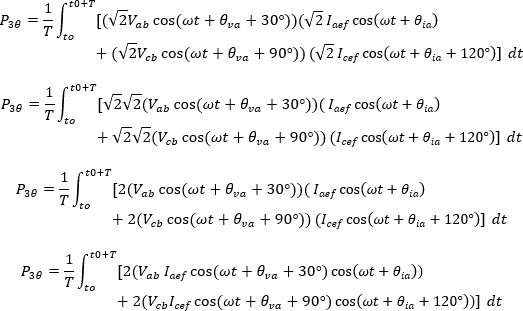
Aplicando la identidad trigonométrica 6.1.5 se tiene:

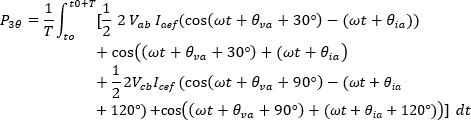
El primer término de la integral para cada vatímetro es independiente del tiempo, por lo tanto, es una constante de la integración.

La segunda integral da como resultado cero, ya que el valor promedio de una onda sinusoidal en un periodo completo es cero; por lo tanto, el segundo término en la ecuación desaparece y la potencia activa trifásica equivale a:

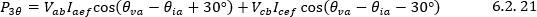
Luego

4.2.2.3 Tercera forma de conexión del método de los 2 elementos o de Aron, utilizando la fase c como referencia.

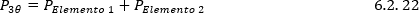
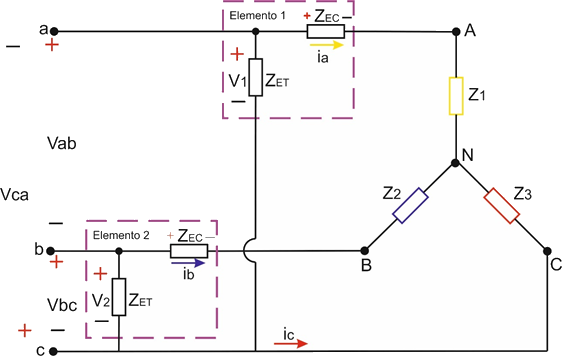
Figura 4.2.8 Método de Aron tercera forma de conexión, fase c de referencia.

Si se reemplaza la corriente 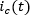en la ecuación de potencia instantánea trifásica para la tercera forma de conexión se tiene que:

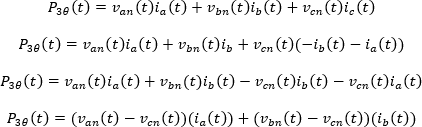
Por lo tanto, la potencia activa trifásica se determina como

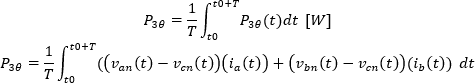
Sustituyendo las ecuaciones de tensión y corriente para cada fase en la ecuación de potencia definida para la fase c se tiene que:

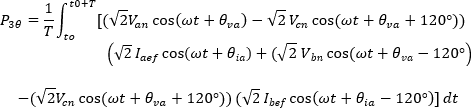
Observemos que en la ecuación anterior se tiene una resta de las tensiones de fase lo cual da como resultado la tensión de línea, a continuación, se realiza dicha operación

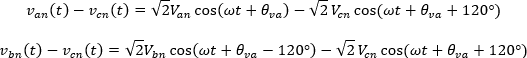
En su forma fasorial se tiene que:

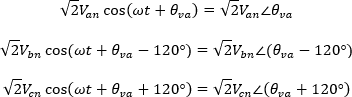
Realizando la resta de tensiones en su forma fasorial:

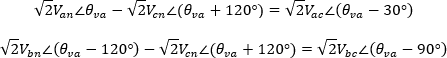
Pasando las ecuaciones del dominio de la frecuencia al dominio del tiempo tenemos:

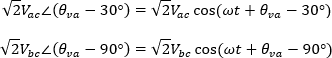
Así la potencia activa se puede expresar como:

Aplicando la identidad trigonométrica 6.1.5 se tiene:

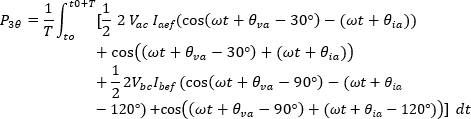
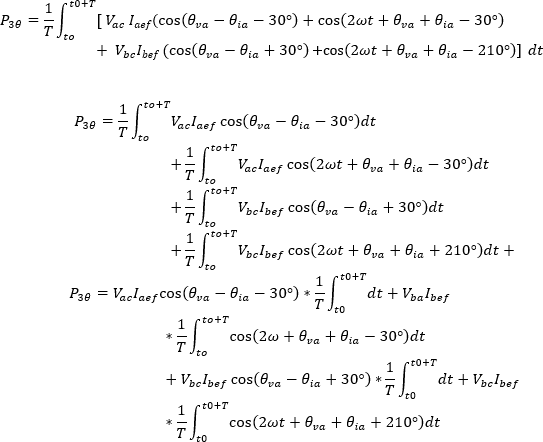
El primer término de la integral para cada vatímetro es independiente del tiempo, por lo tanto, es una constante de la integración.

La segunda integral da como resultado cero, ya que el valor promedio de una onda sinusoidal en un periodo completo es cero; por lo tanto, el segundo término en la ecuación desaparece y la potencia activa trifásica equivale a:

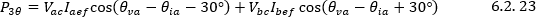
Luego

4.2.1 Método de los tres elementos	4.3 Medición de potencia reactiva trifásica.