3.5.1 Caso general de medición: Análisis de señales usando osciloscopio.

Como ya se especificó, el ángulo de la impedancia representa el desfase entre la tensión que cae en el elemento y la corriente que lo atraviesa. Es posible determinar este ángulo a partir de una medición simultánea de tensión y corriente usando osciloscopio.

La conexión del osciloscopio se realiza de manera similar al esquema de medición de resistencia usando multímetro. En particular se debe tener en cuenta la relación entre el valor de la impedancia a medir, y el valor de la impedancia de entrada del instrumento de medida, lo anterior implica dos posibles formas de conexión:

1. Cuando la impedancia a medir es menor que la impedancia del osciloscopio se puede usar el esquema de conexión sugerido en la figura 3.5.1, en este caso se emplea el Canal A para medición directa de tensión, y el Canal B para medición indirecta de corriente.

Figura 3.5.1 Esquema de conexión de medición de impedancia usando osciloscopio caso 1

Nota: El esquema de conexión sugerido en la figura 3.5.1, no tiene en cuenta la impedancia de las sondas que conectan el osciloscopio y el circuito de ejemplo.

Como se observa en la figura 3.5.1 se elige una única referencia en común para ambos canales, la dirección de las corrientes se asumen de acurdo a la convención pasiva de los signos (corriente de mayor a menor potencial).

Al aplicar la ley de corrientes de Kirchhoff en el nodo b, se determina que:

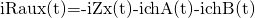
 Ecuación 3.5.7

Si se cumple que Zx<<Zca se tendrá que ichA(t)<<iZx(t) al tener en cuenta las recomendaciones para medición indirecta de corriente con osciloscopio se puede asumir que iZx(t)>>[-ichA(t)-ichB(t)], por tanto:

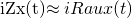
Ecuación 3.5.8

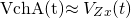
Ecuación 3.5.9

Como se puede observar en la ecuación 3.5.7 y de acuerdo a la ubicación de la referencia del circuito de la figura 3.5.1, resulta necesario invertir la dirección de la corriente iRaux(t) para que tenga el mismo sentido que iZx(t) y así conservar la convención pasiva asignada a la impedancia Zx, por tanto es necesario invertir el Canal B, lo que es equivalente a una inversión de 180° de la señal.

2. Cuando la impedancia a medir es comparable o superior a la impedancia de entrada del osciloscopio se puede usar el método de conexión que se sugiere en la figura 3.5.2, al igual que en el caso anterior se emplea el Canal A para medición directa de tensión, y el Canal B para medición indirecta de corriente.

Figura 3.5.2 Esquema de conexión de medición de impedancia caso 2

Nota: el esquema de conexión sugerido en la figura 3.5.2, no tiene en cuenta la impedancia de las sondas que conectan el osciloscopio y el circuito de ejemplo.

En este esquema de conexiones no es necesario invertir el Canal B si se asume la convención pasiva de los signos que se sugiere en la figura 3.5.2. Al aplicar la ley de tensiones Kirchhoff en la malla indicada se obtiene que:

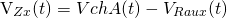
Ecuación 3.5.10

Si se tiene en cuenta las recomendaciones para la medición indirecta de corriente con osciloscopio se asume que ichB(t)<<iRaux(t), por tanto se puede asumir que:

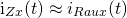
Ecuación 3.5.11

Si Zx>>ZchB se tendrá que VZx(t)>>VZchB(t), por tanto se asume que:

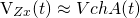
Ecuación 3.5.12

Para los métodos de conexión de la figura 3.5.1 y 3.5.2 el cálculo de la impedancia en un instante de tiempo  se determina de la siguiente manera:

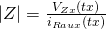
Ecuación 3.5.13

La ecuación 3.5.13 indica que para obtener la magnitud de la impedancia se debe evaluar la señal de tensión y de corriente en un mismo tiempo , tal cálculo se facilita al sistematizar los datos de las formas de onda en Excel, recuerde que:

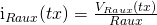
Ecuación 3.5.14

El ángulo de la impedancia se puede calcular al comparar la diferencia de tiempo entre los puntos donde cada forma de onda toca el eje horizontal, por ejemplo observe la figura 3.5.3 la señal se corriente cruzo por en un tiempo ta mientras que la señal de tensión cruzo por cero en un tiempo tb, al determinar que el periodo de ambas señales es T=1/f se calcula el ángulo de desfase como:

Figura 3.5.3 Oscilograma de ejemplo

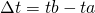
Ecuación 3.5.15

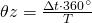
Ecuación 3.5.16

3.5.Medición de Impedancias	3.5.2.Casos particulares de medición