1.3 Operaciones algebraicas básicas de magnitudes con incertidumbre: Suma, resta, multiplicación y división

Las operaciones entre incertidumbres es la forma más rápida y sencilla de aplicar la propagación de la incertidumbre en las cuatro operaciones matemáticas básicas (suma, resta, multiplicación y división). Estas operaciones son de ayuda a la hora de entender la importancia de la propagación de incertidumbre y como afectan en el momento de calcular una nueva variable (variable eléctrica para este caso).

Para explicar de una forma sencilla y aplicada se hablara de estas operaciones en ejemplos comunes de cualquier circuito.

1.3.1 Suma de dos variables

Una suma entre variables es muy común en los nodos o mallas por ejemplo a continuación se hará un análisis en un nodo X aplicando ley de corrientes de Kirchhoff:

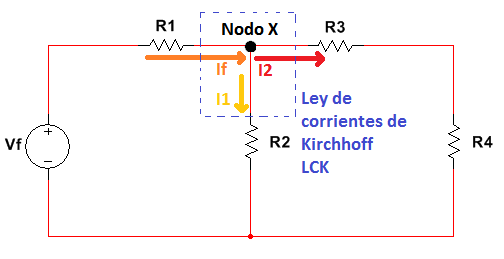
Figura 1.3.1.1 Nodo X y ley de corrientes de Kirchhoff LCK

La ley de corrientes de Kirchhoff es la forma más común para determinar corrientes sobre un nodo, para aplicar la suma en dos variables se calculara el valor de la corriente If:

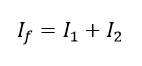
Ecuación 1.3.1.1 Ley de corrientes de Kirchhoff para If

Dónde se posee I1 e I2 poseen sus correspondientes incertidumbres:

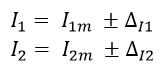
Ecuación 1.3.1.2 Valores de I1 e I2 con sus respectivas incertidumbres

If debería compuesto tanto de su valor medio como de su incertidumbre:

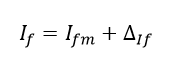
Ecuación 1.3.1.3 Valor medio e incertidumbre de If

Para determinar incertidumbre de la corriente If se aplica la propagación de la incertidumbre:

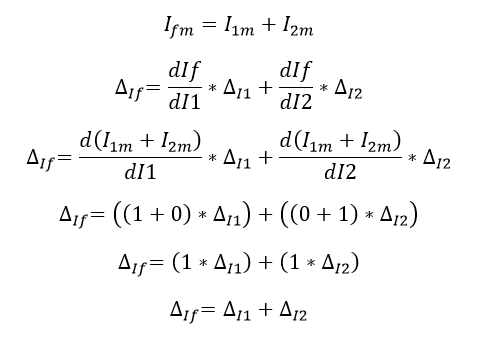
Ecuación 1.3.1.4 Valor medio e incertidumbre de If

Con esto se puede concluir que la propagación en la suma de dos variables la incertidumbre de la variable dependiente (ΔIf) será la suma de las incertidumbres de sus variantes independientes (ΔI1 e ΔI2).

1.3.2 Resta de dos variables

Una resta entre variables es muy común en los nodos o mallas por ejemplo a continuación se hará un análisis en una malla 1 aplicando ley de tensiones de Kirchhoff:

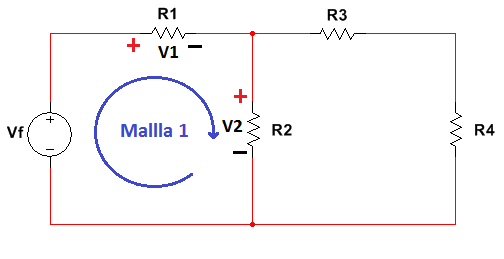
Figura 1.3.2.1 Malla 1 y ley de Tensiones de Kirchhoff LTK

La ley de tensiones de Kirchhoff es la forma más común para determinar tensiones en una malla, para aplicar la resta en dos variables se calculara el valor de la tensión VR1:

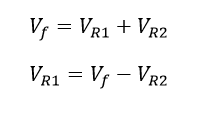
Ecuación 1.3.2.1 Ley de Tensiones de Kirchhoff para VR1

Dónde se posee Vf y VR2 con sus correspondientes incertidumbres:

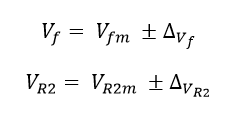
Ecuación 1.3.2.2 Valores de Vf y VR2 con sus respectivas incertidumbres

VR1 debería estar compuesto tanto de su valor medio como de su incertidumbre:

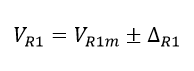
Ecuación 1.3.2.3 Valor medio e incertidumbre de VR1

Para determinar el valor de la incertidumbre se aplicara la propagación de la incertidumbre

Ecuación 1.3.2.4 Valor medio e incertidumbre de VR1

Hay un punto donde la incertidumbre es una resta pero como se explicó en la propagación de la incertidumbre en dos o más variables:

• la incertidumbre total en este caso para VR1 debe ser una suma debido a que es la incertidumbre más grande y por lo tanto es el peor de los casos posibles.

Con esto se puede concluir que la propagación en la suma de dos variables la incertidumbre de la variable dependiente (ΔVR1) será la suma de las incertidumbres de sus variantes independientes (ΔVf y ΔVR2).

1.3.3 Multiplicación de dos variables

Una multiplicación entre variables es muy común usando la ley de ohm la cual es capaz de relacionar voltaje con resistencia y corriente (V=I*R) o potencia eléctrica (P=V*I) por ejemplo a continuación se hará un análisis sobre la resistencia R4 para determinar su potencia eléctrica:

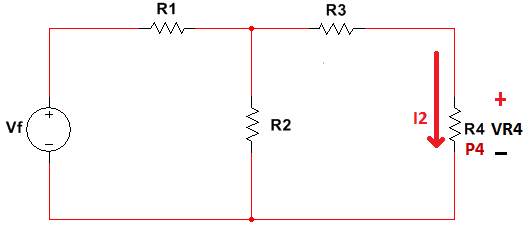
Figura 1.3.3.1 Malla 1 y ley de Tensiones de Kirchhoff LTK

La ley de ohm que relaciona potencia con voltaje y corriente es la forma más común para determinar la potencia sobre un elementó pasivo, para aplicar la multiplicación en dos variables se calculara el valor de la potencia P4:

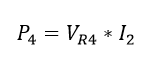
Ecuación 1.3.3.1 Ley de ohm relacionando la potencia P4

Dónde se posee VR4 e I2 con sus correspondientes incertidumbres:

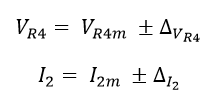
Ecuación 1.3.3.2 Valores de VR4 e I2 con sus respectivas incertidumbres

P4 estará compuesto tanto de su valor medio como de su incertidumbre, la cual será calculada por medio de la propagación de la incertidumbre (derivada de una multiplicación):

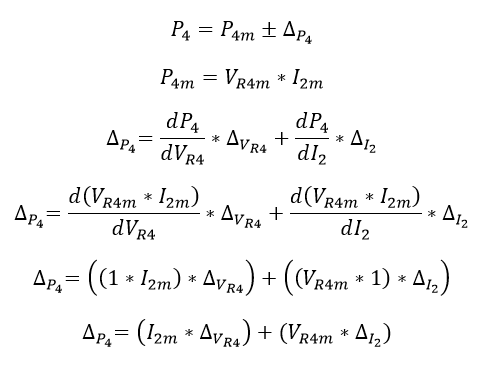
Ecuación 1.3.3.3 Valor medio e incertidumbre de P4

1.3.4 División de dos variables

Una división entre variables es muy común usando la ley de ohm la cual es capaz de relacionar voltaje con resistencia y corriente (V=I*R) o potencia eléctrica (P=V*I) por ejemplo a continuación se hará un análisis sobre la resistencia R4 para determinar su corriente eléctrica:

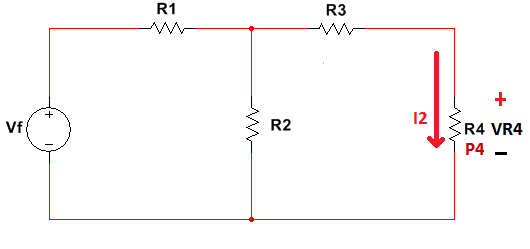
Figura 1.3.4.1 Malla 1 y ley de Tensiones de Kirchhoff LTK

La ley de ohm que relaciona potencia con voltaje y corriente es una forma común para determinar la corriente sobre un elementó pasivo, para aplicar la división en dos variables se calculara el valor de la corriente I2:

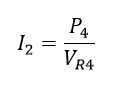
Ecuación 1.3.4.1 Ley de ohm relacionando la corriente I2

Dónde se posee P4 y VR4 con sus correspondientes incertidumbres:

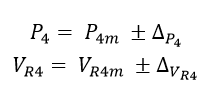
Ecuación 1.3.4.2 Valores de VR4 e I2 con sus respectivas incertidumbres

I2 estará compuesto tanto de su valor medio como de su incertidumbre, la cual será determinada por la propagación de la incertidumbre (derivada de una multiplicación y un cociente):

Ecuación 1.3.4.3 Valor medio e incertidumbre de I2

Conclusiones

• La incertidumbre es el rango donde se encuentra el valor verdadero y el valor medio, en comparación con el error que es una comparación entre valores y este demuestra cuanto se aleja el valor verdadero del valor medido.

• Al poseer una o más variables independientes en una ecuación (es decir que poseen incertidumbre) su valor de incertidumbre afectara y se propagara a la variable que se desea calcular.

• El medio por el que se calcula la propagación de la incertidumbre es por una derivada y se despeja para la incertidumbre deseada (ver propagación de la incertidumbre en una variable).

• Las operaciones básicas demuestran cómo funciona la propagación de la incertidumbre en estas y así ahorrar tiempo a la hora de la aplicación.

 

1.2.2 Incertidumbre Relativa	1.4 Clasificación de los errores