La incertidumbre suele ser un concepto bastante confuso para un estudiante, ya que a simple vista parece complicado y las definiciones dadas por autores llegan a ser algo enrevesadas.
Para simplificar el concepto de incertidumbre y como esta afecta a las demás variables de una función se analizara en los siguientes parámetros, los cuales son necesarios en el área eléctrica en cuanto a mediciones se refiere:
- Incertidumbre.
- Incertidumbre absoluta.
- Incertidumbre relativa.
- Propagación de la incertidumbre.
- Operaciones entre incertidumbres
Incertidumbre en una variable:
El concepto de incertidumbre a primera vista puede parecer muy confuso y dependiendo del área donde se aplique llega a tener un significado distinto; para el caso de la electricidad gracias al texto guía dado por el cronograma de medidas eléctricas de la Universidad Distrital (Barrrera, 2011, pág. 12) afirma que la incertidumbre:"Se considera como el intervalo de valores en donde se tiene certeza que se encuentra tanto el valor medio como el valor verdadero". Estas desviaciones reflejan los cambios y valores que toma el sistema eléctrico.
- Por ejemplo para la medición de 120.0 [V] un equipo "X" puede llegar a desviarse ± 2.0 [V], por lo tanto el rango de operación será desde 118.0 [V] hasta 122.0 [V], es decir que el equipo si realiza una medida adecuada entregara un dato que va desde 118.0 [V] hasta los 122.0 [V] y cualquier valor que se encuentre dentro de estos límites será correcto.
Por otro lado (Centro Español de Metrologia - CEM, 2015) incluye en su definición que: "La incertidumbre de medición comprende, en general, muchas componentes; algunas de ellas pueden evaluarse a partir de la distribución estadística de los resultados de series de medidas, y pueden caracterizarse por desviaciones típicas experimentales". Por lo que la incertidumbre no solo está sujeta a lo que puede llegar a hacer el equipo ya que al fin y al cabo no solo este interviene a la hora de hacer una medición, también se encuentran variables como la presión atmosférica, temperatura del ambiente, temperatura del sistema, comportamiento de los elementos eléctricos, etc.
Gracias a estas definiciones se encuentra que la incertidumbre es un rango de valores, la cual posee:
- Limites superior e inferior
- Un valor medio o central
- Dentro de este rango también se encuentra el valor verdadero (el cual no se puede conocer debido a las diferentes variables implicadas)
A continuación se puede observar un esquema que resume y explica estas afirmaciones:
1.2.1 Comportamiento incertidumbre, por M.A Barreara, 2011, Derechos de autor [2011].
Dónde:
- X0 equivale a la variable medida (voltaje, corriente, potencia, resistencia).
- ΔX equivale a la incertidumbre de la variable medida .
- El valor verdadero del sistema no es posible determinarlo, solo aproximarse a él.
Nota: es importante puntuar que entre este rango se encuentran tanto el valor medio/central o convencionalmente verdadero, el valor de la medición y el valor verdadero del sistema, ya que los cálculos matemáticos demuestran cómo se comporta el sistema idealmente y la medición demuestra cómo se comporta este frente a los diversos elementos y anomalías que pueden llegar a aparecer (presión atmosférica, temperatura, elementos de medición, etc.).
En un equipo de medición se puede encontrar la incertidumbre por medio de su catálogo y la tabla de exactitud, ya que aquí es donde el fabricante informa al operador que tanto se acerca el equipo a realizar una medición óptima.
En otros elementos por ejemplo las resistencias encontramos también catálogos o tablas que indican su tolerancia y cambios de operación dependiendo de diversos factores como por ejemplo temperatura ambiente o voltajes y corrientes de operación.
La incertidumbre puede ser dada de dos formas:
1.2.3 Propagación de la Incertidumbre
La incertidumbre es la forma en que una variable cambia su valor respecto a las diferentes variables que actúan sobre él, por lo tanto una variable posee un valor central (el cual es un punto de referencia) y un rango de operación donde cualquier valor que tome el equipo de medida en este rango será correcto.
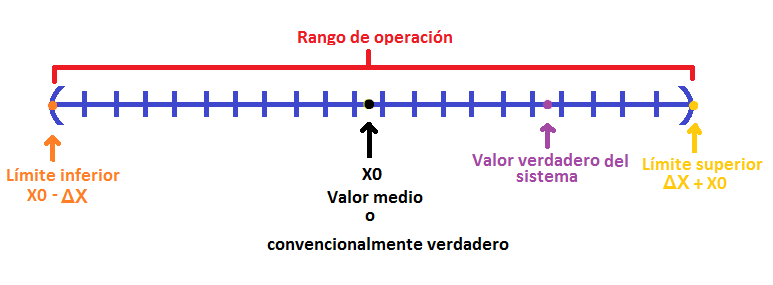
Figura 1.2.3.1 comportamiento incertidumbre, por M.A Barreara, 2011, Derechos de autor [2011].
Por ejemplo para el caso eléctrico la temperatura, elementos del equipo de medición (resistencias, condensadores, batería interna, transistores etc.), conductores y muchas más variables interfieren en obtener un valor que se acerque al valor verdadero del sistema.
Por lo tanto se tienen variables eléctricas que varían su valor dependiendo en cómo se estén comportando las variables que la componen, por esto la incertidumbre se simboliza con el símbolo delta (Δx) que en cálculo diferencial se traduce como razón de cambio o derivada.
Es decir que la incertidumbre son las diferentes derivadas aplicadas a la función a la que se esté evaluando debido a que es la forma en la que puede llegar a cambiar la variable (en este caso de tipo eléctrico) con respecto a los diferentes tipos de variables que influyen en él.
Ahora es fácil de determinar la incertidumbre de una variable medida debido a que el fabricante entrega en su catálogo la exactitud con la que el equipo realiza la medición y como se verá en el tema 2.1.1.3 Exactitud la incertidumbre se determina así:
Para una medición de 250.3 [V] en corriente continua se seleccionan los siguientes datos aportados por el multímetro fluke 179.
Tabla 1.2.3.1 Exactitud
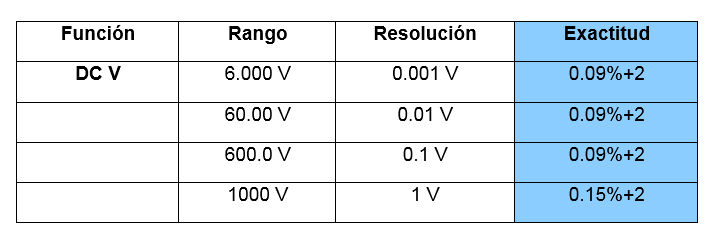
Nota. Recuperado de Fluke Corporation, All rights reserved. Printed in USA
Rango más adecuado para la medición de 250.3 [V] en corriente continua.
Tabla 1.2.3.2 Especificaciones multímetro en función voltímetro D.C
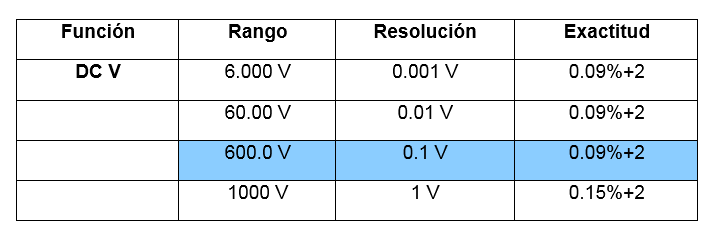
Nota. Recuperado de Fluke Corporation, All rights reserved. Printed in USA
Para determinar que tanto puede desviar la medición el equipo o la incertidumbre del equipo se obtiene la siguiente formula según (Barrrera, 2011, pág. 22):

Ecuación 1.2.3.1 Incertidumbre del equipo
Por lo tanto aplicado a la medición de 250.3 [V] se obtiene el siguiente valor de incertidumbre:
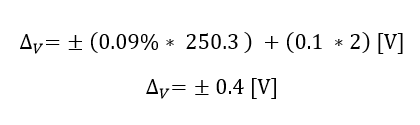
Ecuación 1.2.3.2 Incertidumbre del equipo aplicado
Es decir que gracias a la exactitud dada por el fabricante es fácil determinar la incertidumbre de la medición.
Esto por otro lado cambia para una variable determinada indirectamente ya que no es el equipo de medida el que realiza la medición, sino que matemáticamente se realizan las operaciones convenientes para determinar el valor.
Se le llama Propagación de la incertidumbre a la forma en la que la incertidumbre de una o más variables independientes afecta y se transfieren a una variable calculada teóricamente.
Primero se evaluara la propagación de la incertidumbre en una variable y así poder avanzar en la operación de dos o más variables.
- Propagación de la Incertidumbre en una variable:
A continuación se hará un análisis en un circuito sencillo de forma teórica, esto con el fin de facilitar los cálculos y el análisis del error y tratarlos de forma general y aplicable:
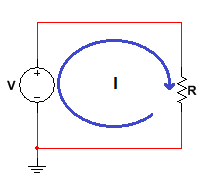
Figura 1.2.3.2 Circuito Sencillo - Análisis Incertidumbre
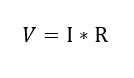
Ecuación 1.2.3.3 Ley de ohm
En este caso se poseen las siguientes condiciones, para así evaluar la incertidumbre con una sola variable independiente:
- Se poseen los valores de una corriente I y una resistencia R.
- gracias al multímetro fluke 179 se obtiene el valor medio e incertidumbre de la corriente I.
- por el contrario R siempre tendrá el mismo valor sin importar con que equipo o en qué condiciones se encuentre siempre se comporta de forma continua.
Vista como una función se comporta de la siguiente manera:
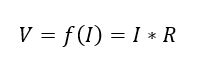
Ecuación 1.2.3.4 Función dependiente - una variable
Es decir se puede definir la tensión V como una función que depende de los cambios de la corriente I, en otras palabras una función f(I).
Recordando las limitaciones impuestas anteriormente se obtienen las siguientes expresiones:
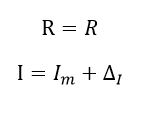
Ecuación 1.2.3.5 Valor medio e incertidumbre de I y R
Para determinar el valor medio de la tensión V simplemente se opera de acuerdo a la ley de ohm como normalmente se hace:
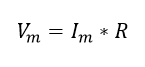
Ecuación 1.2.3.6 Valor medio de V
Por otro lado la incertidumbre es la forma en cómo se comporta y cambia la tensión V en este caso es dependiente del comportamiento de la corriente I, es decir los valores que tome I en determinado momento hace que se modifique el valor final de la tensión V.
El objetivo de una derivada es determinar que tanto cambia una función (en este caso la tensión V por medio de la ley de ohm) con respecto a sus variables independientes (corriente I), es decir que si se deriva la ley de ohm alrededor del valor medio (Vm) se puede observar los valores superior e inferior de Vm e Im (ΔI y ΔV).
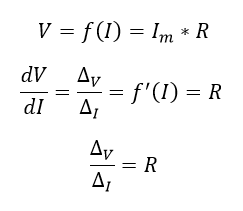
Ecuación 1.2.3.7 Evaluación de la derivada.
Nota: Esto es igual que tener en cálculo diferencial la derivada de una función por ejemplo:
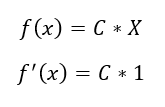
Ecuación 1.2.3.8 Ejemplo calculo diferencial
Donde X es una variable y c es un valor constante.
En este caso X es remplazada por la corriente I y C es remplazada por la resistencia R.
El cambio de la corriente (incertidumbre) es dado por la incertidumbre otorgada por el catalogo del equipo por lo que es posible despejar la incertidumbre o el cambio que presenta la tensión V el cual es el valor de interés a calcular:

Ecuación 1.2.3.9 Incertidumbre de V
Es decir que la incertidumbre para la tensión V viene dada al derivar la función que define su valor medio respecto a la variable independiente que posee incertidumbre (I) multiplicada por la incertidumbre de la corriente I.
Gracias al desarrollo se puede concluir que esto aplica para cualquier tipo de función la cual posea una única variable independiente, dependiendo de únicamente la forma que posea la función o ecuación.
- Incertidumbre en dos o más variables:
Cuando se poseen dos o más variables pasa algo muy similar debido a las propiedades de la derivada, aunque esto es un tema de cálculo multivariado (el cual aún no es un tema que se maneje de acuerdo al pensum), por lo tanto se dará una explicación resumida y sencilla sin tener en cuenta una explicación totalmente teórica partiendo del cálculo en una variable.
Cuando se poseen dos o más variables independientes se aplican derivadas parciales, por ejemplo volviendo al ejemplo de la ley de ohm evaluar a la variable dependiente (V) en cada una de sus variables independientes (I y R):
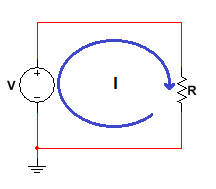
Figura 1.2.3.3 Circuito Sencillo - Análisis Incertidumbre
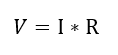
Ecuación 1.2.3.10 Ley de ohm
Considerando en esta ocasión que la tensión V depende de la corriente I y la resistencia R las cuales poseen incertidumbres dadas por el multímetro fluke 179 lo que las hace variables independientes:
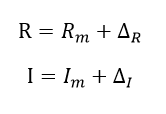
Ecuación 1.2.3.11 Valor medio e incertidumbre de I y R
En este caso la tensión V depende de dos variables independientes, vista como una función se puede ver de la siguiente manera:
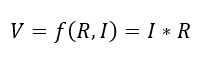
Ecuación 1.2.3.12 Función dependiente - dos variables
La propiedad de las derivadas parciales determina que a la hora de evaluar una función con dos o más variables dependientes se debe evaluar la derivada con respecto a una de ellas y mantener constantes todas las demás, es decir que se poseen dos situaciones:
- Caso 1, la corriente se comporta como variable independiente y todas las demás (R) como constantes:
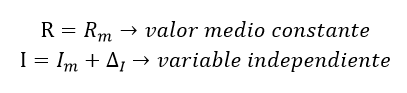
Ecuación 1.2.3.13 Caso 1. Corriente como variable independiente
- Caso 2, resistencia como variable independiente y todas las demás como constantes:
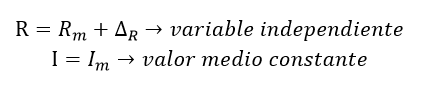
Ecuación 1.2.3.14 Caso 2. Resistencia como variable independiente
Si se realiza el mismo análisis que en la propagación de la incertidumbre se seguirán los mismos pasos ya que solo se poseen funciones con una única variable:
- Caso 1, Derivando respecto a la variable independiente en este caso la corriente I:
Ecuación 1.2.3.15 Caso 1. Incertidumbre para la variable 1 - Corriente
- Caso 2, Derivando respecto a la variable independiente en este caso la Resistencia R:
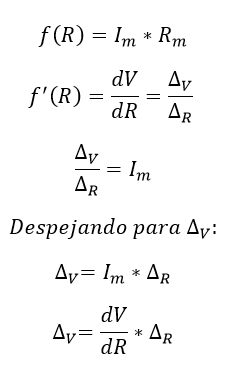
Ecuación 1.2.3.16 Caso 2. Incertidumbre para la variable 2 - Resistencia
Y así se puede continuar para una cantidad indefinida de variables independientes que posea la variable dependiente (que en este caso es la tensión V solo posee dos variables independientes I y R).
Ahora viendo que se poseen dos incertidumbres dadas por las dos variables dependientes (I y R) estas son solo dos fragmentos de una incertidumbre total, por lo tanto para el caso de mediciones eléctricas se sumaran debido a que es la forma de obtener la incertidumbre más grande y por consiguiente es el peor de los casos, por lo que la incertidumbre total para la tensión V será:
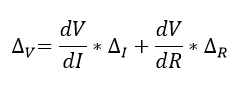
Ecuación 1.2.3.17 Valor total de la incertidumbre de V
Una forma fácil de aprender la forma de la derivada (incertidumbre) es observar respecto a que variable se está derivando, es decir para la primera parte se deriva respecto a la corriente (I) por lo se multiplicara por la incertidumbre de la corriente (ΔI) y así sucesivamente.
De esta forma se puede ampliar la propagación de la incertidumbre para un número indeterminado de variables y además para funciones más complejas (por ejemplo un divisor de tensión).
 |
|
| Contenido |
1.2.1 Incertidumbre Absoluta |
