1.11. Ejercicio Situado 4: Carga - descarga del inductor y medición de la constante de tiempo 5.

La Universidad Francisco José de Caldas reconoce la importancia de las prácticas de laboratorio para las carreras que ofrece, por tal motivo da a conocer a los estudiantes del proyecto curricular de Tecnología en sistemas eléctricos de media y baja tensión, uno de los laboratorios más importantes con el que cuenta, el laboratorio de máquinas eléctricas, donde se puede hacer el montaje de diferentes circuitos eléctricos para analizarlos y obtener un conocimiento menos ideal y lo más cercano a lo real.

Dos estudiantes que se encontraban en dicha presentación, vieron la facilidad que les ofrecía ese laboratorio para realizar la práctica que les había puesto como tarea su profesor de circuitos III, donde debían diseñar un circuito de primer orden RL y analizar el comportamiento de carga y descarga de la bobina y sus variables de tensión y corriente ante una fuente constante, midiendo así mismo su constante de tiempo total, por lo que se disponen a construir su circuito para posteriormente montarlo en el laboratorio de máquinas eléctricas.

Valores nominales cargas:

Para ser precisos, se miden las cargas del Módulo DL1017 DeLorenzo a una frecuencia de operación de 60 Hz utilizando el Puente RLC FLUKE PM6306 (cargas inductivas y capacitivas) y el multímetro FLUKE 289 (carga resistiva) registrando los siguientes valores:

Tabla 5.11.1 Valores nominales de las cargas resistivas Módulo DL1017

Tabla 5.11.2 Valores nominales de las cargas inductivas Módulo DL1017

Equipos disponibles

En las siguientes tablas, se presentan los valores nominales de cada equipo, necesarios para dar solución al presente ejercicio.

• Multímetro FLUKE 289

Con este equipo se medirán las cargas resistivas del módulo DL1017, debido a su baja incertidumbre en las mediciones. También, puede ser utilizado para medir tensiones y corrientes DC/AC, en una amplia variedad de rangos.

Tabla 5.11.3 Especificaciones de resistencia del Multímetro FLUKE 289

• Osciloscopio Rigol DS 1102E

El osciloscopio Rigol es un equipo que permite ver señales de tensión en tiempo real y capturas para señales transitorias. Cuenta con dos canales que permiten la instalación de pinzas amperimétricas y sondas, como lo es la FLUKE i310s que mide corrientes DC/AC, la FLUKE i1000s que solamente mide corrientes AC y la sonda P2220 con la cual se mide la tensión de los elementos de circuito.

Tabla 5.11.4 Especificaciones del Osciloscopio Rigol DS 1102E

• Pinza Amperimétrica FLUKE i310s.

Dicha pinza, internamente tiene un sensor que funciona bajo el principio del efecto hall que detecta corrientes DC y una bobina con la cual se miden corrientes AC. Es de gran utilidad cuando en el mismo circuito se van a medir diferentes corrientes, además ofrece la facilidad de mostrar la señal en un osciloscopio, puesto que tiene una relación de transformación de tensión a corriente.

Tabla 5.11.5 Especificaciones FLUKE i310s AC/DC Current Clamp.

• Puente RLC FLUKE PM6306

El puente RLC facilita la medición de inductancias y capacitancias, entregando información en forma de impedancia (magnitud y ángulo), henrios y microfaradios ya sea en modelo serie o paralelo. Permite, además, hacer las mediciones a diferentes frecuencias.

Tabla 5.11.6 Especificaciones del puente RLC FLUKE PM6306

Diagrama de flujo

Flujograma 4: Análisis de carga-descarga y constante de tiempo (5Τ) de una señal de tensión y corriente en una bobina.

Circuito de primer orden RL objeto de estudio

El siguiente circuito fue diseñado teniendo en cuenta el modelo real de la bobina, en el cual se analizarán variables como corrientes y tensiones tanto en el inductor y su resistencia.

Posible solución

Las cargas elegidas para el circuito fueron tomadas del Módulo de cargas DL1017 del banco DeLorenzo número 4, así: R1 y R2 corresponden a la posición 7, la inductancia en cambio es la serie entre L1,L2 y L3 en posición 1. El interruptor del circuito será un selector con un contacto normalmente abierto (NA).

Figura 5.11.1 Circuito RL para el ejercicio situado 4

Donde la escala de tiempo t se manejará en segundos y 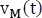es la tensión del modelo completo de la inductancia, es decir, la suma entre y .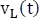

Se debe realizar el respectivo análisis en cada tiempo, para obtener la ecuación de la respuesta natural y forzada de la corriente y tensión, de carga y descarga en el modelo real de la inductancia, las cuales se graficarán, para tener claro lo que se espera ver en el osciloscopio Rigol DS 1102E. Luego, para hallar dichas respuestas, es necesario calcular las constantes de tiempo tau del elemento almacenador de energía, en cada una de las etapas.

Para 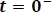: El circuito en este tiempo es el representado en la figura anterior, donde el inductor se encuentra descargado totalmente puesto que ha estado en esa condición mucho tiempo. Entonces, los parámetros de tensión y corriente en la bobina son cero.

Para 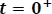: En el contacto NA (normalmente abierto) del selector al ser accionado se cierra y un instante después la bobina se comportará como un circuito abierto, es decir, no permitirá que la condición inicial de carga de la corriente igual a cero, cambie abruptamente; por el contrario, la tensión 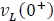si lo hará y será igual en ese instante a .

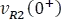Figura 5.11.2 Circuito RL para el ejercicio situado 4 en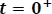

Como se observa en la figura anterior, en el circuito solo fluye corriente por el lazo cerrado de la izquierda, al cual podemos aplicar un divisor de tensión, logrando de esta forma encontrar que .

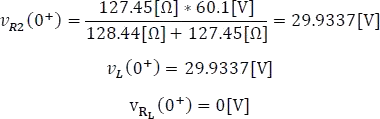
Para : En este intervalo, el inductor tuvo el tiempo suficiente para convertirse en un cortocircuito y la tensión fuese cero, en cambio, la tensión tendría una caída de potencial diferente de cero. La corriente 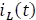a la que llegará la bobina será la impuesta por el circuito en el que está conectada. Esto sucedería, antes de conmutar el selector en .

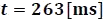Figura 5.11.3 Circuito RL para el ejercicio situado 4 en

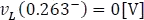
Para hallar la corriente 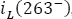, se reduce el circuito anterior haciendo una sumatoria en paralelo entre y a continuación hallando la corriente total del circuito .

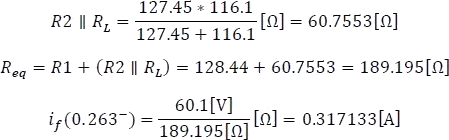
Luego de hallar la corriente de la fuente, se procede a realizar un divisor de tensión, para encontrar la tensión .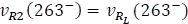

Respuesta completa para la carga de la bobina

Teniendo ya las condiciones iniciales tanto de corriente como de tensión, se puede hallar la respuesta completa para la carga de la bobina; pero antes, se debe hallar la constante de tiempo 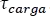, considerando que la resistencia para hallar el tau, es la resistencia equivalente Thevenin del circuito de la Figura 5.11.1 vista desde las terminales de la bobina.

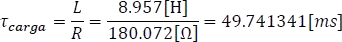
La bobina a los se va a cargar en un 99.3.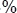

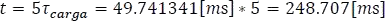
Corriente en el modelo

La forma general de la respuesta completa de la corriente en el inductor ante una entrada DC es:

Donde

La respuesta forzada B para la corriente de la bobina L fue hallada anteriormente como:

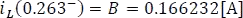
Ahora evaluando la condición inicial en la respuesta completa en

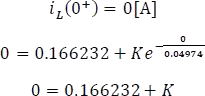
Despejando K

Sustituyendo B, K y a en la ecuación 5.11.1 se tiene,

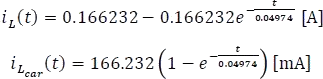
Esta corriente es válida para el modelo serie de la inductancia en la etapa de carga dado que la corriente que fluye es la misma.

Tensión en el modelo

Anteriormente se halló la corriente 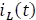, y con ella fácilmente se podría encontrar ; pero, está respuesta solo sería válida si la tensión que se midiera en terminales de ese elemento fuera puramente inductiva. Para este caso específico no es así, porque la medida se realiza en una carga donde la inductancia no es pura, sino que la acompaña una resistencia en serie, este conjunto de elementos es el que se denomina modelo real de la bobina. Por tal motivo, se calculó la respuesta completa para la tensión de la carga, con ayuda de los valores calculados anteriormente para cada condición.

La forma general de la respuesta completa de la tensión en el inductor ante una entrada DC es:

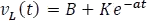
Donde

Como la tensión medida es 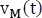, entonces:

La respuesta forzada B para la tensión de la bobina L fue hallada anteriormente como:

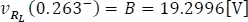
Evaluando la condición inicial en la respuesta completa para

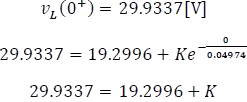
Despejando K

Sustituyendo B,K y a en la ecuación 5.11.2 se tiene,

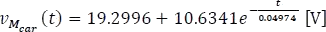
Para : En el selector vuelve a ser operado para abrir de nuevo su contacto, dejando a la bobina conectada con un elemento pasivo más su resistencia interna , y un instante después convertirse en una fuente de corriente, como lo muestra la siguiente figura.

Figura 5.11.4 Circuito RL para el ejercicio situado 4 para

La figura anterior muestra un cambio de polaridad en el inductor, que se debe a que la bobina luego de cargarse y desconectarse de la fuente de alimentación primaria se va a convertir en una fuente de corriente, que no va a cambiar su dirección ni magnitud debido a la característica de no permitir cambios abruptos en la ella, al contrario, su tensión si lo hará, lo que provoca la inversión de la polaridad en la tensión 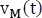en los terminales del elemento, dicho efecto lo explica la Ley de Faraday y Lenz.

Para 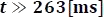: La bobina ya ha entregado toda su energía al elemento pasivo al cual estaba conectado. Por eso todos los parámetros de tensión y corriente en el circuito de la Figura 5.11.4 serán cero.

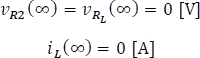
Respuesta completa para la descarga de la bobina

Teniendo ya las condiciones iniciales tanto de corriente como de tensión, se puede hallar la respuesta completa para la descarga de la bobina; pero antes, se debe hallar la constante de tiempo , considerando que la resistencia para hallar el tau, es la resistencia equivalente Thevenin del circuito de la Figura 5.11.4 vista desde las terminales de la bobina que en ese instante será una fuente de corriente.

La bobina a los 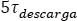se va a cargar en un 99.3.

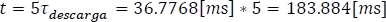
Corriente en el modelo

La forma general de la respuesta completa de la corriente en el inductor ante una entrada DC es:

Donde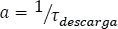

La respuesta forzada B para la corriente de la bobina L fue hallada anteriormente como:

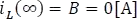
Como la conmutación se hace en la respuesta se traslada a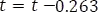

Ahora evaluando la condición inicial en la respuesta completa en

Sustituyendo B, K y a en la ecuación 5.11.3 se tiene,

Esta corriente es válida para el modelo serie de la inductancia en la etapa de descarga dado que la corriente que fluye es la misma.

Tensión en el modelo

Anteriormente se halló la corriente 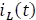, y con ella fácilmente se podría encontrar ; pero, está respuesta no sería válida si la tensión que se midiera en terminales de ese elemento fuera puramente inductiva, debido a que se parte de un análisis anterior y la respuesta sería distinta. Para este caso específico, la medida se realiza en una carga donde la inductancia no es pura, sino que la acompaña una resistencia en serie, este conjunto de elementos es al que se le denomina modelo real de la bobina. Por tal motivo, se calculó la respuesta completa para la tensión de la carga, con ayuda de los valores calculados anteriormente para cada condición.

La forma general de la respuesta completa de la tensión en el inductor ante una entrada DC es:

Donde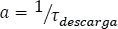

Como la tensión medida es 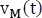, entonces:

La respuesta forzada B para la tensión de la bobina L fue hallada anteriormente como:

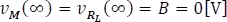
Como la conmutación se hace en la respuesta se traslada a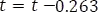

Evaluando la condición inicial en la respuesta completa para

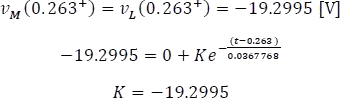
Sustituyendo B,K y a en la ecuación 5.11.4 se tiene,

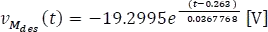
Respuestas completas de la tensión y la corriente de la carga-descarga del inductor

Finalmente se han calculado las respuestas referentes a los parámetros de la bobina de dicho circuito. Ahora se juntarán las respuestas de carga y descarga de la tensión y corriente con una función a trozos como sigue:

Señal de corriente de carga y descarga

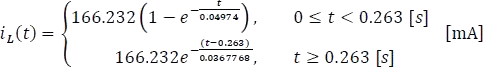
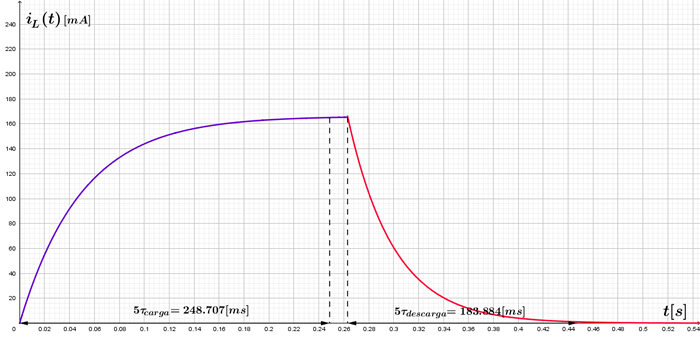
Figura 5.11.5 Respuesta de la corriente del modelo real de la bobina a la carga y a la descarga

Señal de tensión de carga y descarga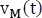

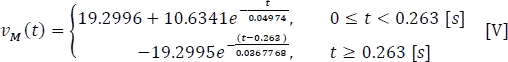
Figura 5.11.6 Respuesta de la tensión del modelo real de la bobina a la carga y a la descarga

Simulación

Luego de realizar el análisis transitorio teórico con cálculos y gráficas de las respuestas de la tensión y la corriente en el inductor del modelo real, se procede a simular el circuito objeto de estudio con el software de simulación NI Multisim 12.0 para comprobar su veracidad.

Se construye el circuito en el espacio de trabajo del programa y se añade el elemento que hará las veces de interruptor con tiempo de retardo como lo muestra la Simulación 5.11.1

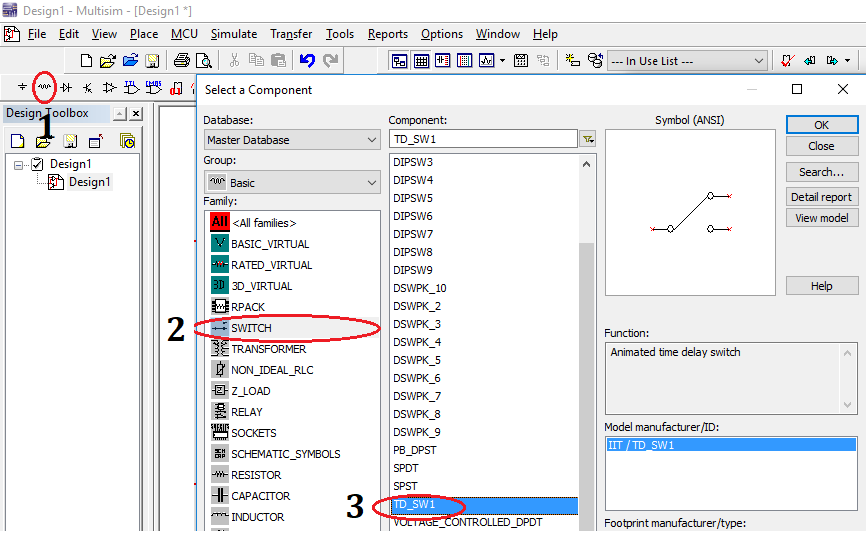
Simulación 5.11.1 Pasos para insertar un interruptor con tiempo de retraso en NI Multisim 12.0

1. Clic en el botón Basic, donde se abrirá una ventana con una lista de los elementos disponibles en esa categoría.

2. Clic en SWITCH, donde se despliega una lista de todos los tipos de este elemento.

3. Clic en TD_SW1, para seleccionar el tipo de interruptor.

4. Finalmente presionar ENTER.

Luego se ubica adecuadamente el elemento con el cursor en el circuito, se procede a conectarlo, se accede a la ventana de parámetros de tiempo de interés y se modifican, como lo muestra la Simulación 5.11.2 ; tal y como se estableció inicialmente en el circuito objeto de estudio.

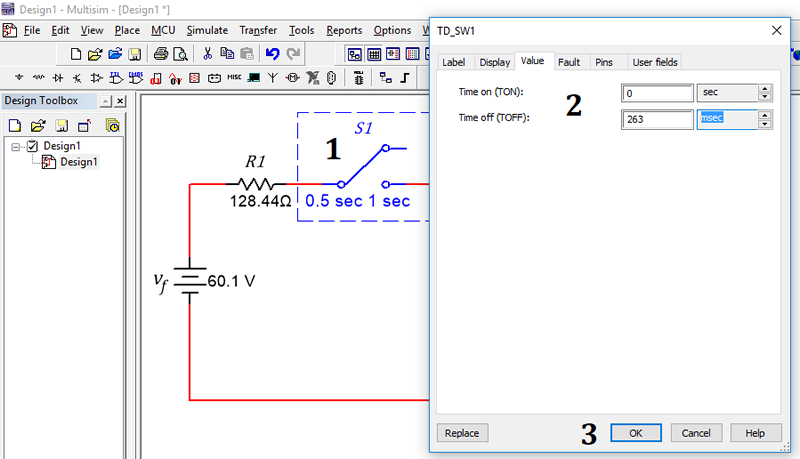
Simulación 5.11.2 Pasos para la configuración de tiempo del interruptor en NI Multisim 12.0

1. Doble clic encima del elemento donde se abrirá una ventana de opciones de configuración.

2. Clic en Value, donde se especifican los tiempos de trabajo.

3. Clic en OK, para guardar la configuración.

Después de realizar todo el montaje en la interfaz, se procede a realizar la simulación del transitorio para las variables de interés, como lo son la corriente y la tensión en el modelo real de la inductancia, mostrado paso a paso en las siguientes figuras.

Obtención de la respuesta de la corriente

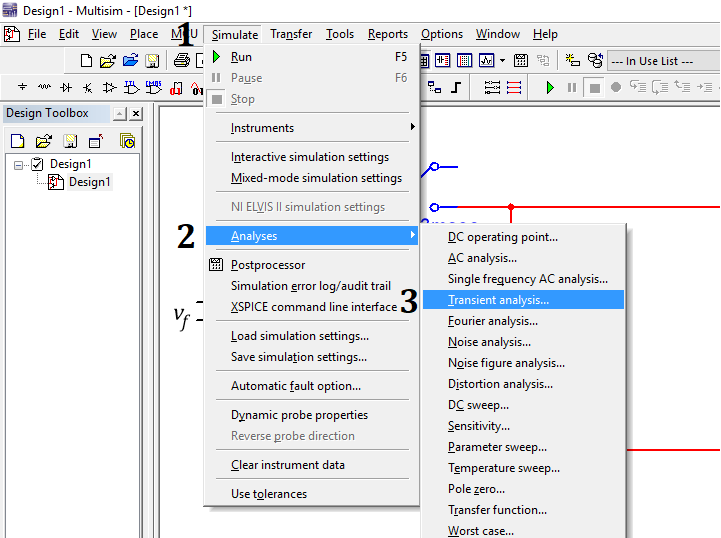
Simulación 5.11.3 Pasos para acceder a la ventana de análisis transitorio

1. Clic en Simulate, donde muestra todas las opciones y herramientas de la simulación.

2. Clic en Analyses, donde se muestra los diferentes tipos de análisis que se pueden implementar en un determinado sistema.

3. Clic en Transient analysis.

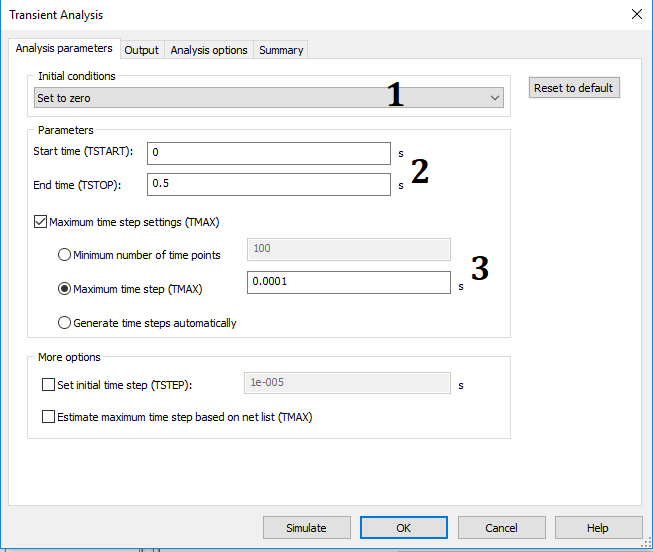
Simulación 5.11.4 Pasos para la configuración de la ventana del menú Parámetros del análisis

1. Desplegar la lista del submenú Initial conditions y elegir la opción Set to zero. Con esto se garantizará que las condiciones del circuito sean nulas.

2. Escribir el tiempo de inicio (TSTART) y parada (TSTOP) de la simulación del transitorio en el submenú Parameters. Con ello se garantizará ver el comportamiento de la corriente de la carga y descarga del modelo real de la bobina.

3. En el mismo submenú Parameters, seleccionar la opción Maximum time step settings (TMAX) y escribir el tiempo de muestreo de datos.

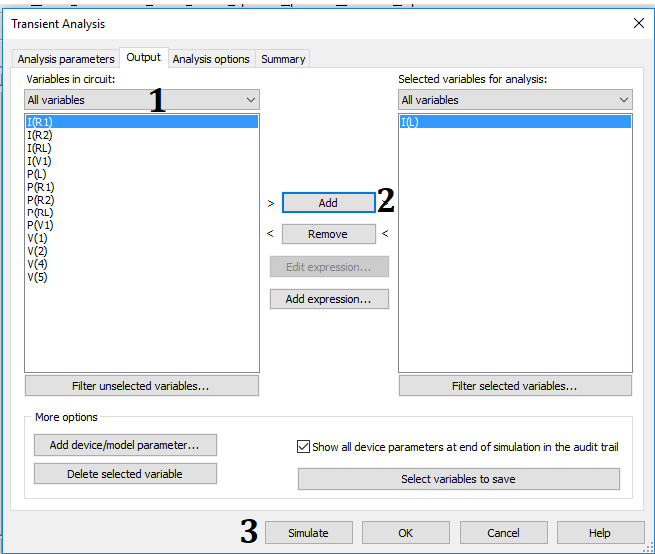
Simulación 5.11.5 Pasos para la configuración de la ventana del menú Salida

1. Desplegar la lista de opciones del submenú Variables in circuit y escoger la opción All variables. Aquí se mostrará la lista de las variables del circuito y se elegirá la de interés dando clic sobre ella.

2. Con la variable elegida, se da clic en el botón Add , para que la variable se traslade a la lista de variables de interés para hacer el análisis y graficar su respuesta.

3. Dar clic en Simulate para iniciar la simulación.

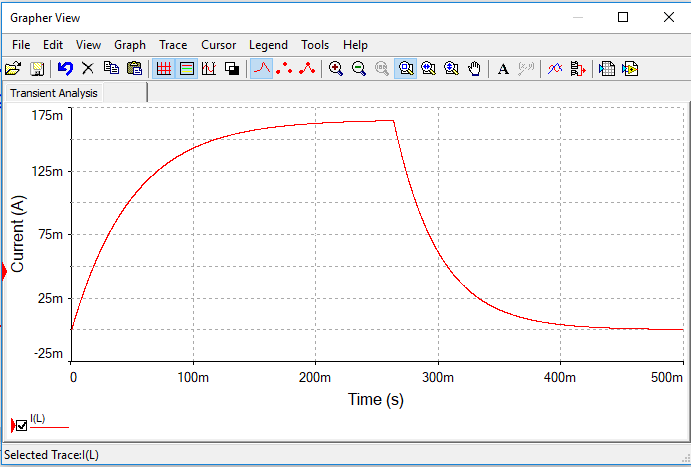
Simulación 5.11.6 Gráfica que muestra el resultado de la simulación de la corriente de la bobina.

Ya estando lista la gráfica, se procede a medir con los cursores el tiempo de carga y de descarga como también el valor de la corriente en cada caso.

Simulación 5.11.7 Pasos para sacar los cursores para la medición del tiempo de carga y descarga

1. Dar clic en en el ícono Show cursors de la barra de herramientas. Sobre el eje vertical aparecerán dos cursores.

2. Los cursores pueden ser desplazados con el ratón, haciendo clic sostenido para medir el tiempo de carga y descarga según convenga.

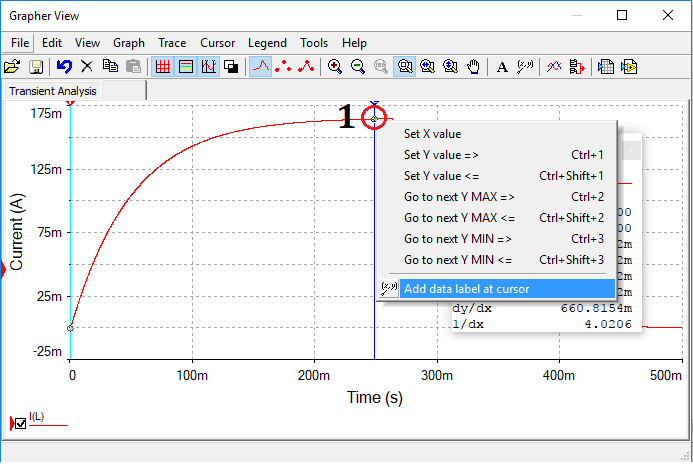
Simulación 5.11.8 Paso para obtener la posición de pareja ordena de tiempo vs miliamperios

1. Dar clic derecho sobre el punto, donde se desplegará una lista y se escoje la última opción Add data label at cursor. Esto permitirá obtener la medición como una pareja ordena del punto, como se muestra en la siguiente figura.

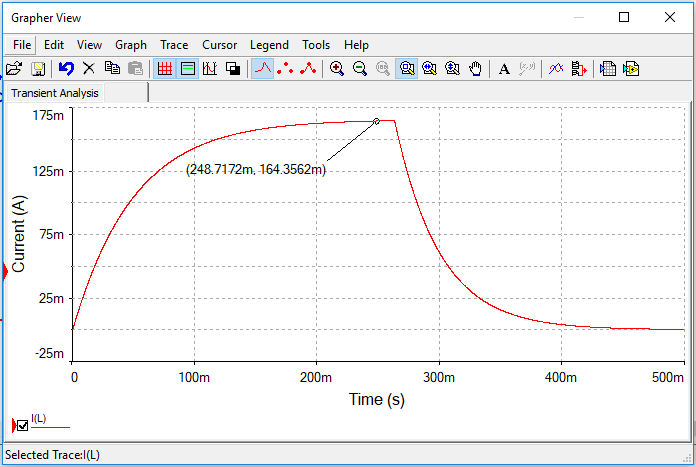
Simulación 5.11.9 Fijación de un punto especial donde se muestra el tiempo y la corriente de carga

Finalmente obtenemos la medición del tiempo de carga y descarga de la corriente como se muestra en la siguiente figura

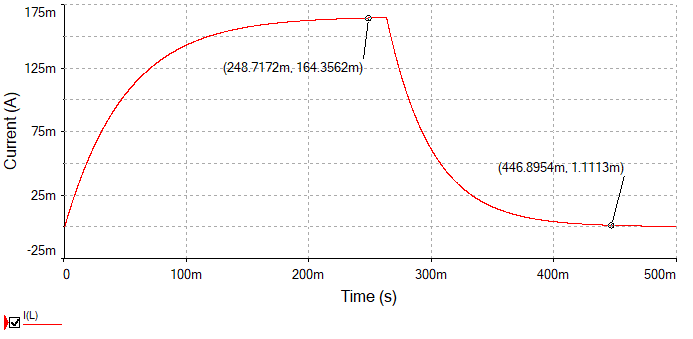
Simulación 5.11.10 Medición de tiempo de carga y descarga de la corriente del modelo real de la bobina

Como se puede observar en la figura anterior, el resultado de la simulación muestra un tiempo de carga de a una corriente de y una duración de descarga que tiene que calcularse como el tiempo registrado de menos el tiempo de la conmutación que son ; lo que da como resultado a una corriente de .

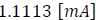Obtención de la respuesta de la tensión

Para la obtención de esta variable se siguen los mismos pasos anteriores, solamente que en la parte de la variable que se le requiere el análisis transitorio será la tensión del modelo real.

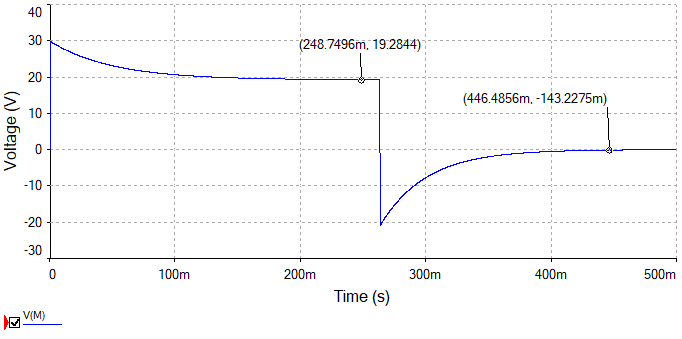
Simulación 5.11.11 Medición de tiempo de carga y descarga de la tensión del modelo real de la bobina

Como se puede observar en la figura anterior, el resultado de la simulación muestra un tiempo de carga de 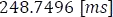a una tensión de 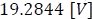y una duración de descarga que tiene que calcularse como el tiempo registrado de 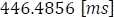menos el tiempo de la conmutación que son ; lo que da como resultado 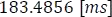a una tensión de .

 

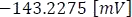Práctica Ejercicio Situado 3: Comportamiento de un circuito de primer orden RC, frente a dos fuentes con señales diferentes.	Práctica Ejercicio Situado 4: Carga - descarga del inductor y medición de la constante de tiempo 5Τ.